
【题目】某校九年级进行立定跳远训练,以下是刘明和张晓同学六次的训练成绩(单位:m)
刘明:2.54,2.48,2.50,2.48,2.54,2.52
张晓:2.50,2.42,2.52,2.56,2.48,2.58
(1)填空:李明的平均成绩是 . 张晓的平均成绩是 .
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?
(3)若预知参加年级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?请说明理由.
【答案】
(1)2.51m,2.51m
(2)解:S2刘明= ![]() ×[(2.54﹣2.51)2+(2.48﹣2.51)2+(2.50﹣2.51)2+(2.48﹣2.51)2+(2.54﹣2.51)2+(2.52﹣2.51)2]≈0.000 63
×[(2.54﹣2.51)2+(2.48﹣2.51)2+(2.50﹣2.51)2+(2.48﹣2.51)2+(2.54﹣2.51)2+(2.52﹣2.51)2]≈0.000 63
S2张晓= ![]() ×[(2.50﹣2.51)2+(2.42﹣2.51)2+(2.52﹣2.51)2+(2.56﹣2.51)2+(2.48﹣2.51)2+(2.58﹣2.51)2]≈0.002 77
×[(2.50﹣2.51)2+(2.42﹣2.51)2+(2.52﹣2.51)2+(2.56﹣2.51)2+(2.48﹣2.51)2+(2.58﹣2.51)2]≈0.002 77
∵S2刘明<S2张晓,
∴刘明的成绩更为稳定.
(3)解:若跳过2.55m就很可能获得冠军,则在6次成绩中,张晓2次都跳过了2.55 m,而刘明一次也没有,所以应选张晓参加.
故答案为:2.51m;2.51m.
【解析】解:(1)刘明的平均成绩为: ![]() ×(2.54+2.48+2.50+2.48+2.54+2.52)=2.51(m)
×(2.54+2.48+2.50+2.48+2.54+2.52)=2.51(m)
张晓的平均成绩为: ![]() ×(2.50+2.42+2.52+2.56+2.48+2.58)=2.51(m)
×(2.50+2.42+2.52+2.56+2.48+2.58)=2.51(m)
(2)S2刘明=![]() ×[(2.54﹣2.51)2+(2.48﹣2.51)2+(2.50﹣2.51)2+(2.48﹣2.51)2+(2.54﹣2.51)2+(2.52﹣2.51)2]≈0.000 63
×[(2.54﹣2.51)2+(2.48﹣2.51)2+(2.50﹣2.51)2+(2.48﹣2.51)2+(2.54﹣2.51)2+(2.52﹣2.51)2]≈0.000 63
S2张晓= ![]() ×[(2.50﹣2.51)2+(2.42﹣2.51)2+(2.52﹣2.51)2+(2.56﹣2.51)2+(2.48﹣2.51)2+(2.58﹣2.51)2]≈0.002 77
×[(2.50﹣2.51)2+(2.42﹣2.51)2+(2.52﹣2.51)2+(2.56﹣2.51)2+(2.48﹣2.51)2+(2.58﹣2.51)2]≈0.002 77
∵S2刘明<S2张晓,
∴刘明的成绩更为稳定.
(3)若跳过2.55m就很可能获得冠军,则在6次成绩中,张晓2次都跳过了2.55 m,而刘明一次也没有,所以应选张晓参加.
所以答案是:(1)2.51m;2.51m(2)刘明的成绩更为稳定;(3)应选张晓参加.
【考点精析】通过灵活运用算术平均数,掌握总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数即可以解答此题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某学校规定学生的学期体育成绩有三部分组成:早锻炼及体育课外活动占10%,体育理论测试占30%,体育技能占60%.王明的三项成绩依次为90分,85分,90分,则王明学期的体育成绩是分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上的位置如图所示,其中点A对应的有理数为-4,且AB=10。动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒(t>0)。
(1)当t=1时,AP的长为 , 点P表示的有理数为;
(2)当PB=2时,求t的值;
(3)M为线段AP的中点,N为线段PB的中点. 在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
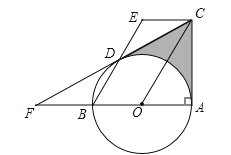
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“防溺水安全知识竞赛”活动,班主任安排班长购买奖品,下面是班长买回奖品时与班主任的对话情况:
班长:买了两种不同的奖品共50件,单价分别为3元和5元,我领了200元,现在找回35元
班主任:你肯定搞错了!
班长:哦!我把自己口袋里的15元一起当作找回的钱款了.
班主任:这就对了!
请根据上面的信息,解决下列问题:
(1)计算两种奖品各买了多少件?
(2)请你解释:班长为什么不可能找回35元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.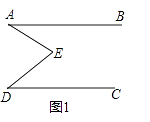
(1)探究猜想:
①若∠A=35°,∠D=30°,则∠AED等于多少度?
②若∠A=48°,∠D=32°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线EF与长方形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求写出证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.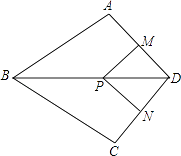
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com