
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.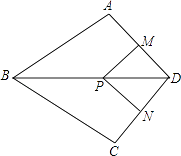
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
【答案】
(1)
证明:∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)
证明:∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
【解析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校九年级进行立定跳远训练,以下是刘明和张晓同学六次的训练成绩(单位:m)
刘明:2.54,2.48,2.50,2.48,2.54,2.52
张晓:2.50,2.42,2.52,2.56,2.48,2.58
(1)填空:李明的平均成绩是 . 张晓的平均成绩是 .
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?
(3)若预知参加年级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李到农贸批发市场了解到苹果和西瓜的价格信息如下:
水果品种 | 苹果 | 西瓜 |
批发价格 | 8元/公斤 | 1.6元/公斤 |
零售价格 | 10元/公斤 | 2元/公斤 |
他共用280元批发了苹果和西瓜共75公斤,
(1)请问小李批发的苹果和西瓜各多少公斤?
(2)若他当天把批发回来的苹果和西瓜按零售价格全部卖出,小李能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°.
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母;
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.
(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬是学校的篮球队长,在一场篮球比赛中,他一人得了25分,其中罚球得了5分,他投进的2分球比3分球多5个,则他本场比赛3分球进了( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2
(1)在直线l上任取两点A,B;
(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;
(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com