
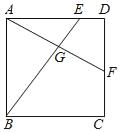
【题目】如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
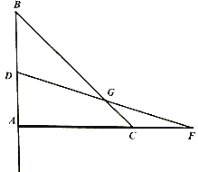
【题目】如图,在等腰![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向运动,同时点
方向运动,同时点![]() 从
从![]() 出发,以相同的速度沿射线
出发,以相同的速度沿射线![]() 方向运动,连
方向运动,连![]() ,交直线
,交直线![]() 于点
于点![]()
![]() 当点
当点![]() 运动到
运动到![]() 中点时,求
中点时,求![]() 的长.
的长.
![]() 求证:
求证:![]() .
.
![]() 过点
过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,请探究
,请探究![]() 之间的数量关系,并直接写出结论.
之间的数量关系,并直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
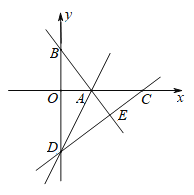
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,点
,点![]() 在
在![]() 轴的负半轴上,若将
轴的负半轴上,若将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴正半轴上的点
轴正半轴上的点![]() 处.
处.
(1)求![]() 的长;
的长;
(2)求点![]() 和点
和点![]() 的坐标;
的坐标;
(3) ![]() 轴上是否存在一点
轴上是否存在一点![]() , 使得
, 使得![]() ?若存在,直接写出点
?若存在,直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
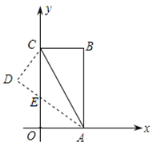
【题目】如图,把长方形纸片![]() 放入平面直角坐标系中,使
放入平面直角坐标系中,使![]() ,
,![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴上,连接
轴上,连接![]() ,将纸片
,将纸片![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 的位置,
的位置,![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
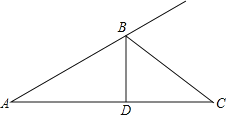
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
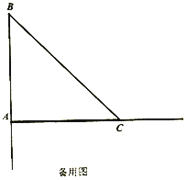
【题目】如图,在△ABC中,BD⊥AC,垂足为C,且∠A<∠C,点E是一动点,其在BC上移动,连接DE,并过点E作EF⊥DE,点F在AB的延长线上,连接DF交BC于点G.
(1)请同学们根据以上提示,在上图基础上补全示意图.
(2)当△ABD与△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润为120元,为了扩大销量,尽快减少库存,超市准备适当降价,据测算,若每箱降价2元,则每天可多售出4箱.
(1)如果要使每天销售该饮料获利14000元,则每箱应降价多少元.
(2)每天销售该饮料获利能达到14500元吗?若能,则每箱应降价多少?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
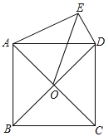
【题目】如图,正方形ABCD的对角线交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE,DE=6,OE=8![]() ,则另一直角边AE的长为_____.
,则另一直角边AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com