
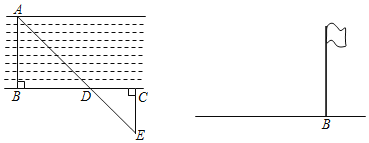
【题目】如图,是方城县潘河的某一段,现要估算河的宽度(即河两岸相对的两点A、B间的距离),可以按如下步骤操作:①先在河的对岸选定一个目标作为点A;②再在河的这一边选定点B和点C,使AB⊥BC;③再选定点E,使EC⊥BC,然后用视线确定BC和AE的交点D.
(1)用皮尺测得BC=177米,DC=61米,EC=50米,求河的宽度AB;(精确到0.1米)
(2)请用所学过的知识设计一种测量旗杆高度AB的方案.
要求:①画出示意图,所测长度用a、b、c等表示,直接标注在图中线段上;
②不要求写操作步骤;③结合所测数据直接用含a、b、c等字母的式子表示出旗杆高度AB.
【答案】(1)两岸间的大致距离AB为95.1m;(2)详见解析.
【解析】
(1)先证明△ABD∽△ECD,然后利用相似比计算AB的长即可;
(2)在旗杆与人之间树立一个标杆,然后利用相似三角形对应边成比例求解.
解:(1)∵AB⊥BC,CE⊥BC,
∴AB∥CE,
∴△ABD∽△ECD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AB≈![]() (m),
(m),
答:两岸间的大致距离AB为![]() m;
m;
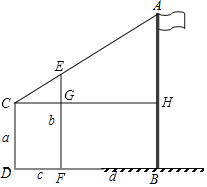
(2)如图,
①将标杆EF立在一个适当的位置;
②人CD站在一个适当的位置:通过标杆的顶部E,刚好看到旗杆的顶部A,
③测出人的身高CD=a,标杆的高度EF=b,人到标杆DF=c的距离和标杆到旗杆FB=d的距离,
④计算旗杆的高度:
过点C作CH⊥AB,交EF于G,交AB于H
易知:CG=DF=c,GF=CD=a,EG=EF-GF=b-a,GH=FB=d,CH=CG+GH=c+d,EF∥AB
∴△CEG∽△CAH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AH=![]()
所以旗杆的高度AB=AH+CD=![]() +a=
+a=![]() .
.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.

(1)求二次函数![]() 的表达式;
的表达式;
(2)过点![]() 作
作![]() 平行于
平行于![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 为抛物线上的一点(点
为抛物线上的一点(点![]() 在
在![]() 上方),作
上方),作![]() 平行于
平行于![]() 轴交
轴交![]() 于点
于点![]() ,当点
,当点![]() 在何位置时,四边形
在何位置时,四边形![]() 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知P(
中,已知P(![]() ,
,![]() ),R(
),R(![]() ,
,![]() )两点,且
)两点,且![]() ,
,![]() ,若过点P作
,若过点P作![]() 轴的平行线,过点R作
轴的平行线,过点R作![]() 轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作
轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作![]() 轴的平行线,过点P作
轴的平行线,过点P作![]() 轴的平行线,两平行线交于一点
轴的平行线,两平行线交于一点![]() ,连接PR,则称△RP
,连接PR,则称△RP![]() 为点R,P,
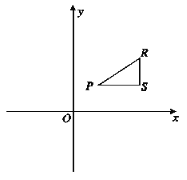
为点R,P,![]() 的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.
的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.
(1)已知点A(0,4),点B(3,0),若△ABC是点A,B,C的“坐标轴三角形”,则点C的坐标为 ;
(2)已知点D(2,1),点E(e,4),若点D,E,F的“坐标轴三角形”的面积为3,求e的值.
(3)若![]() 的半径为
的半径为![]() ,点M(
,点M(![]() ,4),若在
,4),若在![]() 上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求
上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 、
、![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() )重合.
)重合.
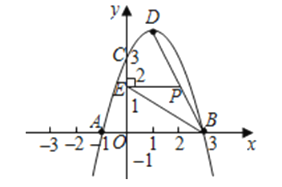
(1)求抛物线的解析式,并写出顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,求
,求![]() 面积的最大值及取得最大值时
面积的最大值及取得最大值时![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,若点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 是抛物线上一动点,试判断是否存在这样的点
是抛物线上一动点,试判断是否存在这样的点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边若存在,请直接写出点
为顶点的四边形是平行四边若存在,请直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
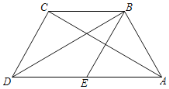
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
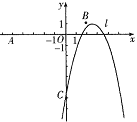
【题目】如图,已知点![]() ,
,![]() ,抛物线
,抛物线![]() :
:![]() (
(![]() 为常数)与
为常数)与![]() 轴的交点为
轴的交点为![]() .
.
(1)经过点![]() ,求它的解析式,并写出此时
,求它的解析式,并写出此时![]() 的对称轴及顶点坐标.
的对称轴及顶点坐标.
(2)设点![]() 的纵坐标为
的纵坐标为![]() ,求
,求![]() 的最大值,此时
的最大值,此时![]() 上有两点(
上有两点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),其中
),其中![]()
![]()
![]()
![]() ,比较
,比较![]() 与
与![]() 的大小;
的大小;
(3)当线段![]() 被
被![]() 只分为两部分,且这两部分的比是1:4时,求
只分为两部分,且这两部分的比是1:4时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com