
【题目】如图,已知点![]() ,
,![]() ,抛物线
,抛物线![]() :
:![]() (
(![]() 为常数)与
为常数)与![]() 轴的交点为
轴的交点为![]() .
.
(1)经过点![]() ,求它的解析式,并写出此时
,求它的解析式,并写出此时![]() 的对称轴及顶点坐标.
的对称轴及顶点坐标.
(2)设点![]() 的纵坐标为
的纵坐标为![]() ,求
,求![]() 的最大值,此时
的最大值,此时![]() 上有两点(
上有两点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),其中
),其中![]()
![]()
![]()
![]() ,比较
,比较![]() 与
与![]() 的大小;
的大小;
(3)当线段![]() 被
被![]() 只分为两部分,且这两部分的比是1:4时,求
只分为两部分,且这两部分的比是1:4时,求![]() 的值.
的值.
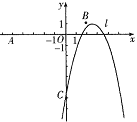
【答案】(1)![]() ,对称轴
,对称轴![]() ,顶点
,顶点![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)
;(3)![]() 的值为0或-5.
的值为0或-5.
【解析】
(1)把点B的坐标代入函数解析式,列出关于h的方程,借助于方程可以求得h的值;利用抛物线函数解析式得到该图象的对称轴和顶点坐标;
(2)把点C的坐标代入函数解析式得到:![]() ,则由二次函数的最值的求法易得yc的最大值,并可以求得此时抛物线的解析式,根据抛物线的增减性来求y1与y2的大小;
,则由二次函数的最值的求法易得yc的最大值,并可以求得此时抛物线的解析式,根据抛物线的增减性来求y1与y2的大小;
(3)根据已知条件“O(0,0),A(5,0),线段OA被l只分为两部分,且这两部分的比是1:4”可以推知把线段OA被l只分为两部分的点的坐标分别是(1,0),(4,0).由二次函数图象上点的坐标特征可以求得h的值.
解:(1)把![]() 代入
代入![]() (或
(或![]() ),
),
对称轴![]() ,顶点
,顶点![]() .
.
(2)点![]() 的横坐标为0,则
的横坐标为0,则![]() ,当
,当![]() 时,
时,![]() 有最大值为1.此时,
有最大值为1.此时,![]() 为
为![]() ,对称轴为y轴,当
,对称轴为y轴,当![]() 时,
时,![]() 随着
随着![]() 的增大而减小,
的增大而减小,
![]() 当
当![]() 时,
时,![]() .
.
(3)把![]() 分1:4两部分的点为(-1,0)或(-4,0).
分1:4两部分的点为(-1,0)或(-4,0).
把![]() 代入
代入![]() 得
得![]() .
.
当![]() 时,
时,![]() 被分为三部分,不合题意,舍去.
被分为三部分,不合题意,舍去.
同理,把![]() 代入
代入![]() 得
得![]() (舍去).
(舍去).
∴h的值为0或-5.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
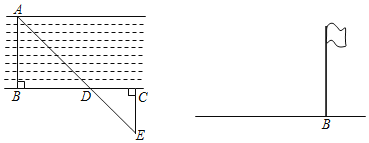
【题目】如图,是方城县潘河的某一段,现要估算河的宽度(即河两岸相对的两点A、B间的距离),可以按如下步骤操作:①先在河的对岸选定一个目标作为点A;②再在河的这一边选定点B和点C,使AB⊥BC;③再选定点E,使EC⊥BC,然后用视线确定BC和AE的交点D.
(1)用皮尺测得BC=177米,DC=61米,EC=50米,求河的宽度AB;(精确到0.1米)
(2)请用所学过的知识设计一种测量旗杆高度AB的方案.
要求:①画出示意图,所测长度用a、b、c等表示,直接标注在图中线段上;
②不要求写操作步骤;③结合所测数据直接用含a、b、c等字母的式子表示出旗杆高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
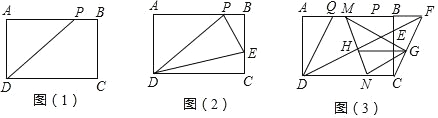
【题目】在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为![]() :1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
:1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
(1)求证:PD=AB.
(2)如图(2),若在“完美矩形“ABCD 的边 BC 上有一动点 E,当![]() 的值是多少时,△PDE 的周长最小?
的值是多少时,△PDE 的周长最小?
(3)如图(3),点 Q 是边 AB 上的定点,且 BQ=BC.已知 AD=1,在(2)的条件下连接 DE 并延长交 AB 的延长线于点 F,连接 CF,G 为 CF 的中点,M、N 分别为线段 QF 和 CD 上的动点,且始终保持 QM=CN,MN 与 DF 相交于点 H,请问 GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地.
(1)A,B间的距离为______km;
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为______km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,![]() ,1,2这六个数字中,随机抽取一个数记为a,则使得关于x的方程
,1,2这六个数字中,随机抽取一个数记为a,则使得关于x的方程![]() =1的解为非负数,且满足关于x的不等式组
=1的解为非负数,且满足关于x的不等式组![]() 只有三个整数解的概率是__.
只有三个整数解的概率是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校其中九年级的3个班学生的捐款金额如下表:

吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:
信息一:这三个班的捐款总金额是7700元;
信息二:二班的捐款金额比三班的捐款金额多300元;
信息三:三班学生平均每人捐款的金额大于49元,小于50元.
请根据以上信息,帮助吴老师解决下列问题:
(1)求出二班与三班的捐款金额各是多少元;
(2)求出三班的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com