
【题目】从﹣2,﹣1,0,![]() ,1,2这六个数字中,随机抽取一个数记为a,则使得关于x的方程
,1,2这六个数字中,随机抽取一个数记为a,则使得关于x的方程![]() =1的解为非负数,且满足关于x的不等式组
=1的解为非负数,且满足关于x的不等式组![]() 只有三个整数解的概率是__.
只有三个整数解的概率是__.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
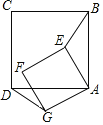
【题目】正方形ABCD和正方形AEFG,AB=12,AE=6![]() .设∠BAE=α(0°≤α≤45°,点E在正方形ABCD内部),BE的延长线交直线DG于点Q.
.设∠BAE=α(0°≤α≤45°,点E在正方形ABCD内部),BE的延长线交直线DG于点Q.
(1)求证:△ADG≌△ABE;
(2)试求出当α由0°变化到45°过程中,点Q运动的路线长,并画出点Q的运动路径;直接写出当α等于多少度时,点G恰好在点Q运动的路径上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是测量一物体体积的过程:
步骤一:将180 mL的水装进一个容量为300 mL的杯子中;
步骤二:将三个相同的玻璃球放入水中,结果水没有满;
步骤三:再将一个同样的玻璃球放入水中,结果水满溢出.

根据以上过程,推测一个玻璃球的体积在下列哪一范围内?(1 mL=1 cm3)( ).
A. 10 cm3以上,20 cm3以下 B. 20 cm3以上,30 cm3以下
C. 30 cm3以上,40 cm3以下 D. 40 cm3以上,50 cm3以下
查看答案和解析>>
科目:初中数学 来源: 题型:
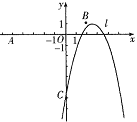
【题目】如图,已知点![]() ,
,![]() ,抛物线
,抛物线![]() :
:![]() (
(![]() 为常数)与
为常数)与![]() 轴的交点为
轴的交点为![]() .
.
(1)经过点![]() ,求它的解析式,并写出此时
,求它的解析式,并写出此时![]() 的对称轴及顶点坐标.
的对称轴及顶点坐标.
(2)设点![]() 的纵坐标为
的纵坐标为![]() ,求
,求![]() 的最大值,此时
的最大值,此时![]() 上有两点(
上有两点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),其中
),其中![]()
![]()
![]()
![]() ,比较
,比较![]() 与
与![]() 的大小;
的大小;
(3)当线段![]() 被
被![]() 只分为两部分,且这两部分的比是1:4时,求
只分为两部分,且这两部分的比是1:4时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(n,3)两点.
(x>0)的图象交于A(m,6),B(n,3)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() >0时x的取值范围.
>0时x的取值范围.
(3)若M是x轴上一点,且△MOB和△AOB的面积相等,求M点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)函数图象上的任意一点P(x,y),y﹣x称为该点的“坐标差”,函数图象上所有点的“坐标差”的最大值称为该函数的“特征值”
(感悟)根据你的阅读理解回答问题:
(1)点P (2,1)的“坐标差”为 ;(直接写出答案)
(2)求一次函数y=2x+1(﹣2≤x≤3)的“特征值”;
(应用)(3)二次函数y=﹣x2+bx+c(bc≠0)交x轴于点A,交y轴于点B,点A与点B的“坐标差”相等,若此二次函数的“特征值”为﹣1,当m≤x≤m+3时,此函数的最大值为﹣2m,求m.
查看答案和解析>>
科目:初中数学 来源: 题型:
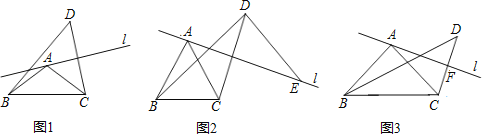
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
(1)如图1,
①求证:点B,C,D在以点A为圆心,AB为半径的圆上.
②直接写出∠BDC的度数(用含α的式子表示)为______.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD.
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转,当线段BF的长取得最大值时,直接写出tan∠FBC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com