Question

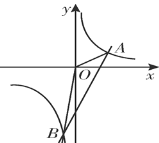
【题目】如图，一次函数y=kx+b与反比例函数y=（x＞0）的图象交于A（m，6），B（n，3）两点．

（1）求一次函数的解析式；

（2）根据图象直接写出kx+b﹣＞0时x的取值范围．

（3）若M是x轴上一点，且△MOB和△AOB的面积相等，求M点坐标．

Answer 1

【答案】（1）一次函数的解析式为y=﹣3x+9；（2）1＜x＜2；（3）点M的坐标为（3，0）或（﹣3，0）．

【解析】

（1）首先求出A、B两点坐标，再利用待定系数法即可解决问题；

（2）观察图象，一次函数的图象在反比例函数的图象上方，写出x的取值范围即可；

（3）设直线AB交x轴于P，则P（3，0），设M（m，0），由S△AOB=S△OBM，可得S△AOP-S△OBP=S△OBM，列出方程即可解决问题．

（1）∵点A（m，6）、B（n，3）在函数图象上，

∴m=1，n=2，

∴A点坐标是（1，6），B点坐标是（2，3），

把（1，6）、（2，3）代入一次函数y=kx+b中，得

，

解得．

∴一次函数的解析式为y=-3x+9；

（2）观察图象可知，kx+b-＞0时x的取值范围是1＜x＜2；

（3）设直线AB交x轴于P，则P（3，0），设M（m，0），

∵S△AOB=S△OBM，

∴S△AOP-S△OBP=S△OBM，

∴，

解得m=±3，

∴点M的坐标为（3，0）或（-3，0）．