
【题目】在平面直角坐标系xOy中,抛物线y=﹣2x2+(m+9)x﹣6的对称轴是x=2.
(1)求抛物线表达式和顶点坐标;
(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A,求点A的坐标;
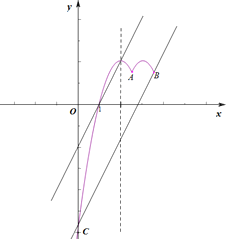
(3)抛物线y=﹣2x2+(m+9)x﹣6与y轴交于点C,点A关于平移后抛物线的对称轴的对称点为点B,两条抛物线在点A、C和点A、B之间的部分(包含点A、B、C)记为图象M.将直线y=2x﹣2向下平移b(b>0)个单位,在平移过程中直线与图象M始终有两个公共点,请你写出b的取值范围 .
【答案】(1)y=﹣2x2+8x﹣6,顶点坐标为(2,2);(2)A (![]() );(3)
);(3)![]() .
.
【解析】
(1)根据抛物线的对称轴公式求出m的值,进而求出抛物线的解析式以及顶点坐标;
(2)先求出平移后的抛物线解析式,然后求出交点坐标;
(3)根据图象即可写出b的取值范围.
(1)∵抛物线y=﹣2x2+(m+9)x﹣6的对称轴是x=2,
∴![]() .
.
∴m=﹣1.
∴抛物线的表达式为y=﹣2x2+8x﹣6.
∴y=﹣2(x﹣2)2+2.
∴顶点坐标为(2,2).
(2)由题意得,平移后抛物线表达式为y=﹣2(x﹣3)2+2,
∵﹣2(x﹣2)2=﹣2(x﹣3)2,
∴![]() .
.
∴A (![]() ).
).
(3)点A坐标为(![]() ),
),
则点B的坐标为![]() ,
,
设直线y=2x﹣2向下平移b(b>0)个单位经过点B,
则y=2x﹣2﹣b,
故![]() =7﹣2﹣b,
=7﹣2﹣b,
解得b=![]() ,
,
设直线y=2x﹣2向下平移b(b>0)个单位经过点A,
![]() =5﹣2﹣b,b=
=5﹣2﹣b,b=![]() ,
,
由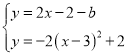 ,消去y得到:2x2﹣10x+14﹣b=0,
,消去y得到:2x2﹣10x+14﹣b=0,
由题意:△=0,
∴100﹣8(14﹣b)=0,
∴b=![]() ,
,
观察图象可知:平移过程中直线与图象M始终有两个公共点,则![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过一点分别作![]() 轴,
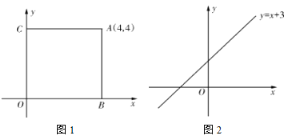
轴,![]() 轴的垂线,若其与两坐标轴围成的矩形的周长与面积相等,则这个点叫做和谐点.例如,图1中过点
轴的垂线,若其与两坐标轴围成的矩形的周长与面积相等,则这个点叫做和谐点.例如,图1中过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() ,矩形
,矩形![]() 的周长为
的周长为![]() ,面积也为
,面积也为![]() ,则点
,则点![]() 是和谐点.
是和谐点.
请根据以上材料回答下列问题:
(1)若点![]() 是和谐点,则
是和谐点,则![]() ______;
______;
(2)若第一象限内的点![]() 与点
与点![]() 均为和谐点,求
均为和谐点,求![]() 的值;
的值;
(3)如图2,若点![]() 为和谐点,且在直线
为和谐点,且在直线![]() 上,求所有满足条件的
上,求所有满足条件的![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 与反比例函数
与反比例函数![]() (x>0)的图象交于点A.将
(x>0)的图象交于点A.将![]() 的图象向下平移6个单位后与双曲线
的图象向下平移6个单位后与双曲线![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
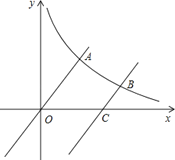
(1)求点C的坐标;
(2)若![]() ,求反比例函数的解析式.
,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(x,y)经过某种变换后到点![]() (-y+1,x+2),我们把点
(-y+1,x+2),我们把点![]() (-y+1,x+2)叫做点P(x,y)的终结点,已知点
(-y+1,x+2)叫做点P(x,y)的终结点,已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() …
…![]() 若点
若点![]() 的坐标为(2,0),则点
的坐标为(2,0),则点![]() 的坐标为_______
的坐标为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:


(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将抛物线![]() 向右平移4个单位长度,平移后的抛物线与y轴的交点为A(0,3),则平移后的抛物线的对称轴为( )
向右平移4个单位长度,平移后的抛物线与y轴的交点为A(0,3),则平移后的抛物线的对称轴为( )
A.x=-1B.x=1C.x=-2D.x=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一方有难,八方支援”是中华民族的传统美德.2月20日13时25分,山西第12批支援武汉医疗队整装出发,在抗击新冠病毒战役中,我省支援湖北医疗队共1500多人奔赴武汉.其中小丽、小王和三个同事共五人直接派往一线某医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到发热门诊,请你利用所学知识完成下列问题.

(1)小丽被派往急诊科的概率是______;
(2)若正好抽出她们一同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com