
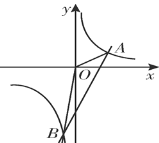
【题目】如图,反比例函数y1=![]() 的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
(1)求反比例函数的表达式;
(2) 当y1﹥y2﹥0时,请直接写出x的取值范围;
(3)连接OA,OB,求△AOB的面积.
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.
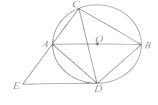
(1)△ABD的面积是________:
(2)求证:DE是⊙O的切线:
(3)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知P(
中,已知P(![]() ,
,![]() ),R(
),R(![]() ,
,![]() )两点,且
)两点,且![]() ,
,![]() ,若过点P作
,若过点P作![]() 轴的平行线,过点R作
轴的平行线,过点R作![]() 轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作
轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作![]() 轴的平行线,过点P作
轴的平行线,过点P作![]() 轴的平行线,两平行线交于一点
轴的平行线,两平行线交于一点![]() ,连接PR,则称△RP
,连接PR,则称△RP![]() 为点R,P,
为点R,P,![]() 的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.
的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.
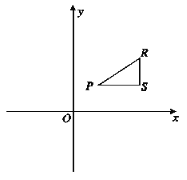
(1)已知点A(0,4),点B(3,0),若△ABC是点A,B,C的“坐标轴三角形”,则点C的坐标为 ;
(2)已知点D(2,1),点E(e,4),若点D,E,F的“坐标轴三角形”的面积为3,求e的值.
(3)若![]() 的半径为
的半径为![]() ,点M(
,点M(![]() ,4),若在
,4),若在![]() 上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求
上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
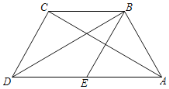
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
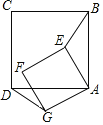
【题目】正方形ABCD和正方形AEFG,AB=12,AE=6![]() .设∠BAE=α(0°≤α≤45°,点E在正方形ABCD内部),BE的延长线交直线DG于点Q.
.设∠BAE=α(0°≤α≤45°,点E在正方形ABCD内部),BE的延长线交直线DG于点Q.
(1)求证:△ADG≌△ABE;
(2)试求出当α由0°变化到45°过程中,点Q运动的路线长,并画出点Q的运动路径;直接写出当α等于多少度时,点G恰好在点Q运动的路径上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(n,3)两点.
(x>0)的图象交于A(m,6),B(n,3)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() >0时x的取值范围.
>0时x的取值范围.
(3)若M是x轴上一点,且△MOB和△AOB的面积相等,求M点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com