
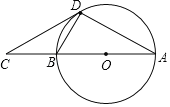
【题目】如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠A=∠BDC;
(2)若![]() =
=![]() ,AC=3,求CD的长.
,AC=3,求CD的长.
【答案】(1)详见解析;(2)2.
【解析】
(1)要证明∠A=∠BDC,只要求出∠ODC=∠BDA即可,根据题目中的条件,不难得到∠ODC=∠BDA=90°,∠ODB=∠OBD,从而可以证明结论成立;
(2)要求CD的长,只要证明△CDB∽△CAD即可,然后根据![]() ,AC=3,即可求得CD的长.
,AC=3,即可求得CD的长.
(1)连接OD.
∵CD是⊙O的切线,点C在直径AB的延长线上,
∴∠ODC=90°,∠BDA=90°,OB=OD,
∴∠ODB+∠BDC=90°,∠OBD+∠A=90°,∠ODB=∠OBD,
∴∠A=∠BDC;
(2)∵∠DCB=∠ACD,∠BDC=∠DAC,
∴△CDB∽△CAD,
∴![]() ,
,
∵![]() ,AC=3,
,AC=3,
∴![]() ,
,
∴CD=2,
即CD的长是2.



科目:初中数学 来源: 题型:
【题目】某学校在倡导学生大课间活动中,随机抽取了部分学生对“我最喜爱课间活动”进行了一次抽样调查,分别从打篮球、踢足球、自由活动、跳绳、其它等5个方面进行问卷调(每人只能选一项),根据调查结果绘制了如图的不完整统计图,请你根据图中信息,解答下列问题.

(1)本次调查共抽取了学生 人;
(2)求本次调查中喜欢踢足球人数;
(3)若甲、乙两位同学通过抽签的方式确定自己填报的课间活动,则两位同学抽到同一运动的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)如果果园既要让橙子的总产量达到60375个,又要确保每一棵橙子树接受到的阳光照射尽量少受影响,那么应该多种多少棵橙子树?
(2)增种多少棵橙子树,可以使果园橙子的总产量最多?最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
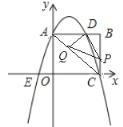
【题目】如图1,抛物线 ![]() 经过
经过 ![]() ,
, ![]() 两点,与
两点,与 ![]() 轴相交于点
轴相交于点 ![]() ,连接
,连接 ![]() .点
.点 ![]() 为抛物线上一动点,过点
为抛物线上一动点,过点 ![]() 作
作 ![]() 轴的垂线
轴的垂线 ![]() ,交直线
,交直线 ![]() 于点
于点 ![]() ,交
,交 ![]() 轴于点
轴于点 ![]() .
.
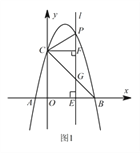
Ⅰ 求抛物线的表达式;
Ⅱ 当 ![]() 位于
位于 ![]() 轴右边的抛物线上运动时,过点
轴右边的抛物线上运动时,过点 ![]() 作
作 ![]() 直线
直线 ![]() ,
, ![]() 为垂足.当点
为垂足.当点 ![]() 运动到何处时,以
运动到何处时,以 ![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似?并求出此时点
相似?并求出此时点 ![]() 的坐标;
的坐标;
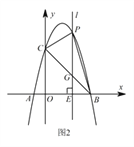
Ⅲ 如图2,当点 ![]() 在位于直线
在位于直线 ![]() 上方的抛物线上运动时,连接
上方的抛物线上运动时,连接 ![]() ,
, ![]() .请问
.请问 ![]() 的面积
的面积 ![]() 能否取得最大值?若能,请求出最大面积
能否取得最大值?若能,请求出最大面积 ![]() ,并求出此时点
,并求出此时点 ![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
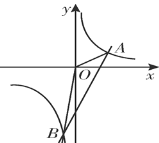
【题目】如图,反比例函数y1=![]() 的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
(1)求反比例函数的表达式;
(2) 当y1﹥y2﹥0时,请直接写出x的取值范围;
(3)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.已知一组正方形的四个顶点恰好落在两坐标轴上,请你观察每个正方形四条边上的整点的个数的变化规律.回答下列问题:
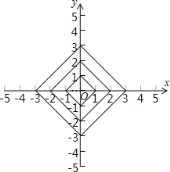
(1)经过x轴上点(5,0)的正方形的四条边上的整点个数是________;
(2)经过x轴上点(n,0)(n为正整数)的正方形的四条边上的整点个数为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为(4,3),抛物线
的坐标为(4,3),抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点.
两点.
(1)求抛物线的表达式;
(2)点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 运动,与此同时,点
运动,与此同时,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,当其中一点到达终点时,另一点也停止运动.连接
运动,当其中一点到达终点时,另一点也停止运动.连接![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).
①当![]() 为何值时,
为何值时,![]() 得面积最小?
得面积最小?
②是否存在某一时刻![]() ,使
,使![]() 为直角三角形?若存在,直接写出
为直角三角形?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋中有四个小球,分别标有数字1、2、3、4,它们除了数字外都相同。第一次从中摸出一个小球,记录数字后放回袋中,第二次摇匀后再随机摸出一个小球.
(1)求第一次摸出的小球所标数字是偶数的概率;
(2)求两次摸出的小球所标数字相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com