
����Ŀ����ͼ������![]() �У�
�У�![]() Ϊԭ�㣬��
Ϊԭ�㣬��![]() ��
��![]() ���ϣ���
���ϣ���![]() ��
��![]() ���ϣ���
���ϣ���![]() ������Ϊ��4,3����������
��������4,3����������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����ֱ��
����ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() �ύ��
�ύ��![]() ����.
����.
��1���������ߵı���ʽ��
��2����![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ����ÿ��1����λ���ȵ��ٶ����
����ÿ��1����λ���ȵ��ٶ����![]() �˶������ͬʱ����
�˶������ͬʱ����![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ����ÿ��
����ÿ��![]() ����λ���ȵ��ٶ����
����λ���ȵ��ٶ����![]() �˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶�.����
�˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶�.����![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() ���룩.
���룩.
�ٵ�![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() �������С��
���������
���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() Ϊֱ�������Σ������ڣ�ֱ��д��
Ϊֱ�������Σ������ڣ�ֱ��д��![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
���𰸡���1��![]() ����2����
����2���� ![]() ����
����![]()
��������
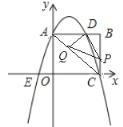
��1�����ݵ�B������ɵó���A��C�����꣬���������߽���ʽ�������b��c��ֵ����������ߵĽ���ʽ��
��2���ٹ���Q��P��QF��AB��PG��AC������ֱ�ΪF��G���Ƴ���QFA�ס�CBA����CGP�ס�CBA���ú�t��ʽ�ӱ�ʾOF��PG���������ε�����ú�t��ʽ�ӱ�ʾ��������϶��κ��������ʿ������ֵ��������������ֱ�ǵ�λ�ò�ȷ�������������ۣ����ݵ�����꣬�ٽ�������ľ��빫ʽ�ù��ɶ�����⼴�ɣ�
�⣺��1��������֪��A(0,3),C(4,0)��
�������߾���A��B���㣬
��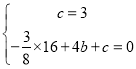 ����ã�
����ã�![]() ��
��
�������ߵı���ʽΪ��![]() ��
��
(2)�� ���ı���ABCD�Ǿ��Σ�
���B=90O�� ��AC2=AB2+BC2=5��
��![]() ���ɵ�
���ɵ�![]() ����D��2,3����
����D��2,3����
����Q��P��QF��AB��PG��AC������ֱ�ΪF��G��
�ߡ�FAQ=��BAC�� ��QFA=��CBA��
���QFA�ס�CBA��
��![]() ��
��
��![]() ��
��
ͬ������CGP�ס�CBA��
��![]() ��
��![]() ����
����![]() ��
��
![]()
![]()
��![]() ʱ����DPQ�������С.��СֵΪ
ʱ����DPQ�������С.��СֵΪ![]() ��
��
�� ��ͼ���֪��D������Ϊ(2,3)��AC=5,ֱ��AC�Ľ���ʽΪ��![]() ��
��
������ֱ�ǵ�λ�ò�ȷ�������������ۣ�
��![]() ʱ�����ݹ��ɶ����ɵó���
ʱ�����ݹ��ɶ����ɵó���
![]() ��
��
�������ⷽ�̼��ɵý⣻
��![]() ʱ����֪��G�˶�����B��λ�ã���P�˶���C��λ�ã�����ʱ��Ϊt=3��
ʱ����֪��G�˶�����B��λ�ã���P�˶���C��λ�ã�����ʱ��Ϊt=3��
��![]() ʱ,ͬ���ù��ɶ����ó���
ʱ,ͬ���ù��ɶ����ó���
![]() ��
��
�������ɵ�t��ֵ��
�ɴ˿ɵó�t��ֵΪ��![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
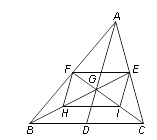
����Ŀ����ͼ����ABC������AD��BE��CF�ཻ�ڵ�G��H��I�ֱ���BG��CG���е㣮
��1����֤���ı���EFHI��ƽ���ı��Σ�
��2���ٵ�AD��BC�������� ʱ���ı���EFHI�Ǿ��Σ�
�ڵ�AD��BC�������� ʱ���ı���EFHI�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
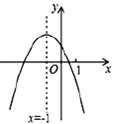
����Ŀ�����κ���![]() ��ͼ����ͼ�����н��ۣ���
��ͼ����ͼ�����н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() .��ȷ�ĸ���Ϊ�� ��
.��ȷ�ĸ���Ϊ�� ��
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
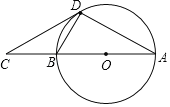
����Ŀ����ͼ��CD����O�����ߣ���C��ֱ��AB���ӳ����ϣ�
��1����֤����A����BDC��
��2����![]() ��
��![]() ��AC��3����CD�ij���
��AC��3����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�BDΪһ���Խ��ߣ�AD��BC��AD��2BC����ABD��90�㣬EΪAD���е㣬����BE��
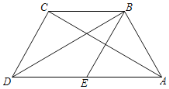
��1����֤���ı���BCDEΪ���Σ�
��2������AC����ACƽ�֡�BAD��AB��2��������BCDE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
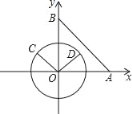
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��4��0������B��0��4��������C���뾶Ϊ2����O�ϣ�����OC����O����OD��OC��OD����O�ཻ�ڵ�D������AB��
��1������C�ڵڶ�������O���˶�����OC��ABʱ����BOC�Ķ���Ϊ������
��2������C��������O���˶�������C�˶���ʲôλ��ʱ����ABC�������������ABC����������ֵ��
��3������C�ڵ�һ����������O���˶�������AD����OC��ADʱ��
�������C�����ꣻ
��ֱ��BC�Ƿ�Ϊ��O�����ߣ��������жϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
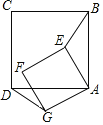
����Ŀ��������ABCD��������AEFG��AB��12��AE��6![]() �����BAE����(0�������45�㣬��E��������ABCD�ڲ�)��BE���ӳ��߽�ֱ��DG�ڵ�Q��
�����BAE����(0�������45�㣬��E��������ABCD�ڲ�)��BE���ӳ��߽�ֱ��DG�ڵ�Q��
��1����֤����ADG�ա�ABE��
��2�������������0��仯��45������У���Q�˶���·�߳�����������Q���˶�·����ֱ��д���������ڶ��ٶ�ʱ����Gǡ���ڵ�Q�˶���·���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Dz���һ��������Ĺ��̣�
����һ����180 mL��ˮװ��һ������Ϊ300 mL�ı����У�
���������������ͬ�IJ��������ˮ�У����ˮû������
���������ٽ�һ��ͬ���IJ��������ˮ�У����ˮ�����.

�������Ϲ��̣��Ʋ�һ��������������������һ��Χ�ڣ�(1 mL=1 cm3)(����).
A. 10 cm3���ϣ�20 cm3���� B. 20 cm3���ϣ�30 cm3����
C. 30 cm3���ϣ�40 cm3���� D. 40 cm3���ϣ�50 cm3����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������壩����ͼ���ϵ�����һ��P��x��y����y��x��Ϊ�õ�����������������ͼ�������е����������������ֵ��Ϊ�ú�����������ֵ��
������������Ķ�����ش����⣺
��1����P ��2��1�������������Ϊ�� ������ֱ��д���𰸣�
��2����һ�κ���y��2x+1����2��x��3����������ֵ����
��Ӧ�ã���3�����κ���y����x2+bx+c��bc��0����x���ڵ�A����y���ڵ�B����A���B�������������ȣ����˶��κ�����������ֵ��Ϊ��1����m��x��m+3ʱ���˺��������ֵΪ��2m����m��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com