
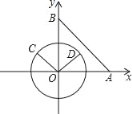
【题目】如图,在平面直角坐标系中,已知点A(4,0),点B(0,4),动点C在以半径为2的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D,连接AB.
(1)若点C在第二象限的⊙O上运动,当OC∥AB时,∠BOC的度数为 ;
(2)若点C在整个⊙O上运动,当点C运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值;
(3)若点C在第一、二象限的⊙O上运动,连接AD,当OC∥AD时,
①求出点C的坐标;
②直线BC是否为⊙O的切线?请作出判断,并说明理由.
【答案】(1)45°;(2)4![]() +8;(3)①点C在第一象限时,C(
+8;(3)①点C在第一象限时,C(![]() ,1);②直线BC是⊙O的切线.
,1);②直线BC是⊙O的切线.
【解析】
(1) 根据题意可得△OAB为等腰直角三角形,所以∠ABO=∠BAO=![]()
(2)由三角形面积公式可得当点C运动到第三象限的角平分线与⊙ 0的交点位置时,点C与AB的距离为最大值, 即△ABC的面积最大,由勾股定理可得AB的长,根据直角三角形中线定理可得OE=5AB, 再由三角形面积公式计算即可.
(3)1由平行线的性质和相似三角形的判定可得△C'OF~△ODA,由相似三角形的性质可得![]() ,再由勾股定理可得OF的长,即可求得点C'的坐标.
,再由勾股定理可得OF的长,即可求得点C'的坐标.
2(2)根据题意由SAS证明△BOC≌△AOD,∠BCO=∠ADO=90°,得直线BC是⊙O的切线.
解:(1)∵点A(4,0),点B(0,4),
∴OA=OB=4,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴∠BOC=∠OBA=45°,
故答案为45°.
(2)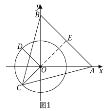
当点C到AB的距离最大时,△ABC的面积最大,
如图1,过点O作OE⊥AB于E,OE的反向延长线交⊙O
于C',此时,点C'到AB的距离最大,最大值为C'E的长,
∵△OAB是等腰直角三角形,
∴AB=![]() OA=4
OA=4![]() ,
,
∴OE=![]() AB=2
AB=2![]() ,
,
∴CE=OC'+OE=2+2![]() ,
,
∴△ABC的面积为![]() C'E×AB=4
C'E×AB=4![]() +8,
+8,
即:当点C在⊙O上运动到第三象限的角平分线与⊙O的交点的位置时,
△ABC的面积最大,最大值为4![]() +8;
+8;
(3)①如图2,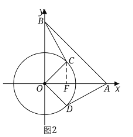
当点C为位于第二象限时,
过点C作CF⊥x轴于F,
∵OD⊥OC,OC∥OD,∴
∠ADO=∠COD=90°,
∴∠DOA+∠DAO=90°,
∵∠DOA+∠COF=90°,
∴∠COF=∠DAO,
∴△OCF∽△AOD,
∴![]() ,
,
∴![]() ,
,
∴CF=1,
在Rt△OCF中,根据勾股定理得,OF=![]() ,
,
∴C(﹣![]() ,1),
,1),
同理:点C在第一象限时,C(![]() ,1);
,1);
②直线BC是⊙O的切线,
理由:当点C在第二象限时,
在Rt△OCF中,OC=2,CF=1,
∴∠COF=30°,
∴∠OAD=30°,
∴∠BOC=60°,
∴∠AOD=60°,
在△BOC和△AOD中,![]() ,
,
∴△BOC≌△AOD,
∴∠BCO=∠ADO=90°,
∴OC⊥BC,
∴直线BC为⊙O的切线;
同理:当点C在第一象限时,直线BC为⊙O的切线,
即:当OC∥AD时,直线BC是⊙O的切线.


科目:初中数学 来源: 题型:
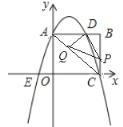
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线 ![]() 经过
经过 ![]() ,
, ![]() 两点,与
两点,与 ![]() 轴相交于点
轴相交于点 ![]() ,连接
,连接 ![]() .点
.点 ![]() 为抛物线上一动点,过点
为抛物线上一动点,过点 ![]() 作
作 ![]() 轴的垂线
轴的垂线 ![]() ,交直线
,交直线 ![]() 于点
于点 ![]() ,交
,交 ![]() 轴于点
轴于点 ![]() .
.
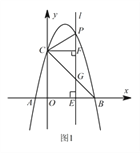
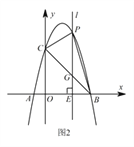
Ⅰ 求抛物线的表达式;
Ⅱ 当 ![]() 位于
位于 ![]() 轴右边的抛物线上运动时,过点
轴右边的抛物线上运动时,过点 ![]() 作
作 ![]() 直线
直线 ![]() ,
, ![]() 为垂足.当点
为垂足.当点 ![]() 运动到何处时,以
运动到何处时,以 ![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似?并求出此时点
相似?并求出此时点 ![]() 的坐标;
的坐标;
Ⅲ 如图2,当点 ![]() 在位于直线
在位于直线 ![]() 上方的抛物线上运动时,连接
上方的抛物线上运动时,连接 ![]() ,
, ![]() .请问
.请问 ![]() 的面积
的面积 ![]() 能否取得最大值?若能,请求出最大面积
能否取得最大值?若能,请求出最大面积 ![]() ,并求出此时点
,并求出此时点 ![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.已知一组正方形的四个顶点恰好落在两坐标轴上,请你观察每个正方形四条边上的整点的个数的变化规律.回答下列问题:
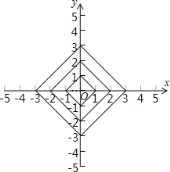
(1)经过x轴上点(5,0)的正方形的四条边上的整点个数是________;
(2)经过x轴上点(n,0)(n为正整数)的正方形的四条边上的整点个数为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为(4,3),抛物线
的坐标为(4,3),抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点.
两点.
(1)求抛物线的表达式;
(2)点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 运动,与此同时,点
运动,与此同时,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,当其中一点到达终点时,另一点也停止运动.连接
运动,当其中一点到达终点时,另一点也停止运动.连接![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).
①当![]() 为何值时,
为何值时,![]() 得面积最小?
得面积最小?
②是否存在某一时刻![]() ,使
,使![]() 为直角三角形?若存在,直接写出
为直角三角形?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
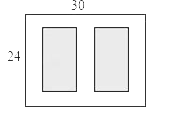
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋中有四个小球,分别标有数字1、2、3、4,它们除了数字外都相同。第一次从中摸出一个小球,记录数字后放回袋中,第二次摇匀后再随机摸出一个小球.
(1)求第一次摸出的小球所标数字是偶数的概率;
(2)求两次摸出的小球所标数字相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
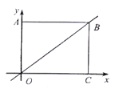
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 分别在坐标轴的正半轴上,
分别在坐标轴的正半轴上, ![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与折线
与折线![]() 有公共点.
有公共点.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)对于一次函数![]() ,当
,当![]() 随
随![]() 的增大而减小时,直接写出
的增大而减小时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
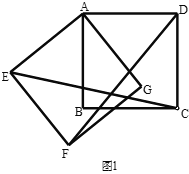
【题目】已知:正方形![]() 绕点
绕点![]() 顺时针旋转至正方形
顺时针旋转至正方形![]() ,连接
,连接![]() .
.
(1)如图,求证:![]() ;
;
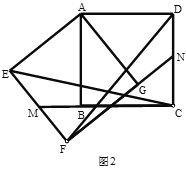
(2)如图,延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com