
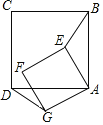
【题目】正方形ABCD和正方形AEFG,AB=12,AE=6![]() .设∠BAE=α(0°≤α≤45°,点E在正方形ABCD内部),BE的延长线交直线DG于点Q.
.设∠BAE=α(0°≤α≤45°,点E在正方形ABCD内部),BE的延长线交直线DG于点Q.
(1)求证:△ADG≌△ABE;
(2)试求出当α由0°变化到45°过程中,点Q运动的路线长,并画出点Q的运动路径;直接写出当α等于多少度时,点G恰好在点Q运动的路径上.
【答案】(1)证明见解析;(2)图见解析;![]() .
.
【解析】
(1)由正方形的性质得出AD=AB,AG=AE,∠EAG=∠BAD=90°,易证∠DAG=∠BAE,由SAS证得△ADG≌△ABE;
(2)由△ADG≌△ABE,得出∠ADG=∠ABE,则∠BQD=∠BAD=90°,得出点Q的运动轨迹是以BD为直径的![]() ,所对的圆心角是90°,BD=
,所对的圆心角是90°,BD=![]() AB=12
AB=12![]() ,则点Q的运动路径长=
,则点Q的运动路径长=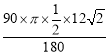 =3
=3![]() π,由AE=6
π,由AE=6![]() ,得出AE=AG=
,得出AE=AG=![]() BD=OD,当B、E、G三点共线,且OG=OD时,Q与G重合,则△OAG是等边三角形,得出∠GAO=60°,推出∠BAE=∠DAG=60°﹣45°=15°,即可得出结果.
BD=OD,当B、E、G三点共线,且OG=OD时,Q与G重合,则△OAG是等边三角形,得出∠GAO=60°,推出∠BAE=∠DAG=60°﹣45°=15°,即可得出结果.
(1)证明:∵四边形ABCD与四边形AEFG是正方形,
∴AD=AB,AG=AE,∠EAG=∠BAD=90°,
∴∠DAG+∠DAE=∠BAE+∠DAE=90°,
∴∠DAG=∠BAE,
在△ADG和△ABE中,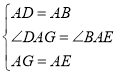 ,
,
∴△ADG≌△ABE(SAS);
(2)解:∵△ADG≌△ABE,
∴∠ADG=∠ABE,
∴∠BQD=∠BAD=90°,
∴点Q的运动轨迹是以BD为直径的![]() ,所对的圆心角是90°,
,所对的圆心角是90°,
∵AB=12,
∴BD=![]() AB=12
AB=12![]() ,
,
∴点Q的运动路径长=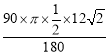 =3
=3![]() π,
π,
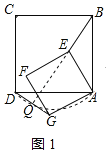
点Q的运动路径如图1所示:
∵AE=6![]() ,
,
∴AE=AG=![]() BD=OD,
BD=OD,
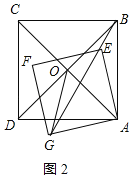
当B、E、G三点共线,且OG=OD时,Q与G重合,如图2所示:
则△OAG是等边三角形,
∴∠GAO=60°,
∵∠DAC=45°,
∴∠BAE=∠DAG=60°﹣45°=15°,
∴当α=15°时,点G恰好在点Q运动的路径上.


科目:初中数学 来源: 题型:
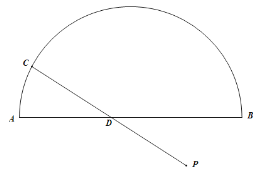
【题目】如图,![]() 是直径AB所对的半圆弧,点P是
是直径AB所对的半圆弧,点P是![]() 与直径AB所围成图形的外部的一个定点,AB=8cm,点C是
与直径AB所围成图形的外部的一个定点,AB=8cm,点C是![]() 上一动点,连接PC交AB于点D.
上一动点,连接PC交AB于点D.
小明根据学习函数的经验,对线段AD,CD,PD,进行了研究,设A,D两点间的距离为x cm,C,D两点间的距离为![]() cm,P,D两点之间的距离为
cm,P,D两点之间的距离为![]() cm.
cm.
小明根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0.00 | 1.00 | 2.00 | 3.00 | 3.20 | 4.00 | 5.00 | 6.00 | 6.50 | 7.00 | 8.00 |
| 0.00 | 1.04 | 2.09 | 3.11 | 3.30 | 4.00 | 4.41 | 3.46 | 2.50 | 1.53 | 0.00 |
| 6.24 | 5.29 | 4.35 | 3.46 | 3.30 | 2.64 | 2.00 | m | 1.80 | 2.00 | 2.65 |
补充表格;(说明:补全表格时,相关数值保留两位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,并画出函数
中,描出补全后的表中各组数值所对应的点,并画出函数![]() 的图象:
的图象:
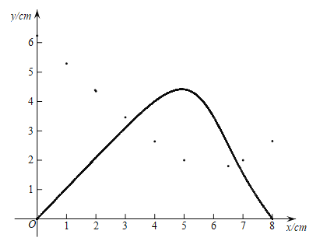
(3)结合函数图象解决问题:当AD=2PD 时,AD的长度约为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
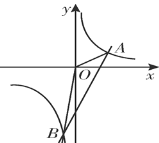
【题目】如图,反比例函数y1=![]() 的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
(1)求反比例函数的表达式;
(2) 当y1﹥y2﹥0时,请直接写出x的取值范围;
(3)连接OA,OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
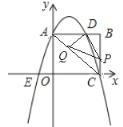
轴上,点![]() 的坐标为(4,3),抛物线
的坐标为(4,3),抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点.
两点.
(1)求抛物线的表达式;
(2)点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒1个单位长度的速度向点
上以每秒1个单位长度的速度向点![]() 运动,与此同时,点
运动,与此同时,点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,当其中一点到达终点时,另一点也停止运动.连接
运动,当其中一点到达终点时,另一点也停止运动.连接![]() ,设运动时间为
,设运动时间为![]() (秒).
(秒).
①当![]() 为何值时,
为何值时,![]() 得面积最小?
得面积最小?
②是否存在某一时刻![]() ,使
,使![]() 为直角三角形?若存在,直接写出
为直角三角形?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
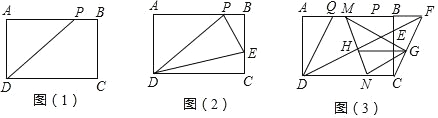
【题目】在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为![]() :1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
:1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
(1)求证:PD=AB.
(2)如图(2),若在“完美矩形“ABCD 的边 BC 上有一动点 E,当![]() 的值是多少时,△PDE 的周长最小?
的值是多少时,△PDE 的周长最小?
(3)如图(3),点 Q 是边 AB 上的定点,且 BQ=BC.已知 AD=1,在(2)的条件下连接 DE 并延长交 AB 的延长线于点 F,连接 CF,G 为 CF 的中点,M、N 分别为线段 QF 和 CD 上的动点,且始终保持 QM=CN,MN 与 DF 相交于点 H,请问 GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋中有四个小球,分别标有数字1、2、3、4,它们除了数字外都相同。第一次从中摸出一个小球,记录数字后放回袋中,第二次摇匀后再随机摸出一个小球.
(1)求第一次摸出的小球所标数字是偶数的概率;
(2)求两次摸出的小球所标数字相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,![]() ,1,2这六个数字中,随机抽取一个数记为a,则使得关于x的方程
,1,2这六个数字中,随机抽取一个数记为a,则使得关于x的方程![]() =1的解为非负数,且满足关于x的不等式组
=1的解为非负数,且满足关于x的不等式组![]() 只有三个整数解的概率是__.
只有三个整数解的概率是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣2x2+(m+9)x﹣6的对称轴是x=2.
(1)求抛物线表达式和顶点坐标;
(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A,求点A的坐标;
(3)抛物线y=﹣2x2+(m+9)x﹣6与y轴交于点C,点A关于平移后抛物线的对称轴的对称点为点B,两条抛物线在点A、C和点A、B之间的部分(包含点A、B、C)记为图象M.将直线y=2x﹣2向下平移b(b>0)个单位,在平移过程中直线与图象M始终有两个公共点,请你写出b的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com