
����Ŀ��Ԫ������У�С�ģ�С����С����λͬѧ���ڰ���Ե�����������������������Ϸ����������ʦ���ˣ�С��������������ʦ�μӣ���Ϸ�������£�����λͬѧ�����ӱ��������ڽ������룬����Χ��������Ȧ���ߣ������߹����в���Ա�����ͣ��������ͣ��������Ѹ��������һ�������ϣ�û�����������ӵ�����̭�����ܽ�����һ����Ϸ.
��1�������¼��DZ�Ȼ�¼����� .
A������ʦ����̭ B��С���������Լ�����������
C��С��������С������������ D������λͬѧ���Խ�����һ����Ϸ
��2���������ʦû���������κ�һ�����ӣ���λͬѧ�������������ӵ���û���������Լ����������ӣ���Ϊ�¼�![]() ��������¼�
��������¼�![]() �ĸ��ʣ�������״ͼ�����б�������˵��.
�ĸ��ʣ�������״ͼ�����б�������˵��.
���𰸡���1��D����2��ͼ��������![]()
��������
��1����������¼�����Ȼ�¼��Ͳ������¼��Ķ������ɵã�
��2���������⻭����״ͼ�г����еȿ��ܽ�����ٸ��ݸ��ʹ�ʽ���ɵã�
�⣺��1��![]() ������ʦ����̭������¼���
������ʦ����̭������¼���![]() ��С���������Լ�����������������¼���
��С���������Լ�����������������¼���
![]() ��С��������С������������������¼���
��С��������С������������������¼���![]() ������3�����ӣ�������ֻ��1λ��ʦ������һ����2λͬѧ�ܽ�����һ����Ϸ�����DZ�Ȼ�¼�.
������3�����ӣ�������ֻ��1λ��ʦ������һ����2λͬѧ�ܽ�����һ����Ϸ�����DZ�Ȼ�¼�.
��ѡ��![]() ��
��
��2���⣺��С�ģ�С����С����λͬѧ������������������Ϊa��b��c��
����״ͼ����
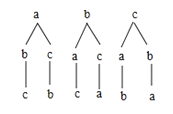
����״ͼ��֪�����еȿ��ܽ������6�֣����е�4�֡���5�ֽ���������⣬
��P��A����![]() .
.


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b�뷴��������y=![]() ��x��0����ͼ����A��m��6����B��n��3�����㣮
��x��0����ͼ����A��m��6����B��n��3�����㣮
��1����һ�κ����Ľ���ʽ��
��2������ͼ��ֱ��д��kx+b��![]() ��0ʱx��ȡֵ��Χ��
��0ʱx��ȡֵ��Χ��
��3����M��x����һ�㣬����MOB����AOB�������ȣ���M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
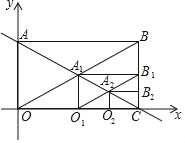
����Ŀ����ͼ��ֱ��y��![]() ��x��y��ֱ���A��C���㣬��ACΪ�Խ�������һ������ABCO���Խ��߽���ΪA1������CA1Ϊ�Խ������ڶ�������A1B1CO1���Խ��߽���ΪA2��ͬ��������������A2B2CO2�Խ��߽���ΪA3�����Դ����ƣ����2019�����ζԽ��߽���A2019������Ϊ_____��
��x��y��ֱ���A��C���㣬��ACΪ�Խ�������һ������ABCO���Խ��߽���ΪA1������CA1Ϊ�Խ������ڶ�������A1B1CO1���Խ��߽���ΪA2��ͬ��������������A2B2CO2�Խ��߽���ΪA3�����Դ����ƣ����2019�����ζԽ��߽���A2019������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
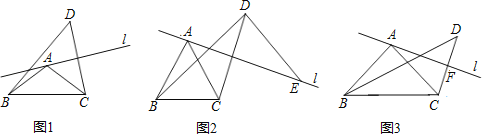
����Ŀ����֪�ڡ�ABC�У�AB��AC����BAC������ֱ��l������A(��������B���C)����C����ֱ��l�ĶԳƵ�Ϊ��D������BD��CD.
(1)��ͼ1��
����֤����B��C��D���Ե�AΪԲ�ģ�ABΪ�뾶��Բ��.
��ֱ��д����BDC�Ķ���(�ú�����ʽ�ӱ�ʾ)Ϊ______.
(2)��ͼ2��������60��ʱ������D��BD�Ĵ�����ֱ��l���ڵ�E����֤��AE��BD.
(3)��ͼ3��������90��ʱ����ֱ��l��CD�Ľ���ΪF������BF.��ֱ��l�Ƶ�A��ת�����߶�BF�ij�ȡ�����ֵʱ��ֱ��д��tan��FBC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ����������֧�����������������������������������ǵ���������˺ܶ������������ѧС����У�ڶ��������Ͽɵ��Ĵ��������������е��飬���������m�ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��

��1������ͼ����Ϣ���m=�� ����n=�� ����
��2������������ǽ�������ͳ��ͼ��ȫ��
��3�����ݳ�������Ľ���������ȫУ2000��ѧ���У���Լ�ж��������Ͽ���������һ�������
��4����֪A��B��λͬѧ�����Ͽ���������Cͬѧ���Ͽ���֧������Dͬѧ���Ͽ�����������������ͬѧ�г�ȡ����ͬѧ������ͨ����״ͼ������������λͬѧ���Ͽɵ��������ﲻһ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
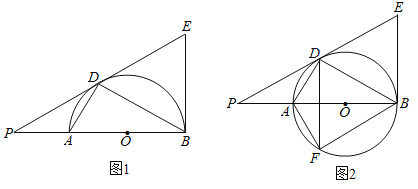
����Ŀ����ͼ��AB��ԲO��ֱ����OΪԲ�ģ�AD��BD�ǰ�Բ���ң��ҡ�PDA=��PBD���ӳ�PD��Բ������BE�ڵ�E
��1��֤����ֱ��PD�ǡ�O������.
��2�������BED=60�㣬![]() ����PA�ij���
����PA�ij���
��3�����߶�PD��ֱ��ADΪ�Գ������Գ��߶�DF����F������ԲO�ϣ���ͼ2����֤���ı���DFBEΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��һ��ֱ��ˮƽ��Ľ����ijͬѧ�ӽ������B����������ˮƽ������������20�����C���پ���һ���¶ȣ����±ȣ�Ϊi=1��0.75���³�Ϊ10��б��CD�����D��Ȼ������ˮƽ������������40�����E��A��B��C��D��E����ͬһƽ���ڣ�����E����ý����ﶥ��A������Ϊ24����������AB�ĸ߶�ԼΪ���ο����ݣ�sin24���0.41��cos24���0.91��tan24��=0.45����������

A. 21.7�� B. 22.4�� C. 27.4�� D. 28.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����������ʩ��һ����Ͷ�ʹ�˾�ⶨ��ij�����ò軨���¼�����һƬ�˹����������г����飬����![]() ��軨��
��軨��![]() ���¼��ķ�����ͬ������
���¼��ķ�����ͬ������![]() ��軨��
��軨��![]() ���¼�����
���¼�����![]() Ԫ.
Ԫ.
��1����軨���¼������۵��ۣ�
��2���þ���������Ҫ�軨�¼���![]() �꣬Ҫ��軨���¼���
�꣬Ҫ��軨���¼���![]() �꣬���������ֻ����ܷ��ò�����
�꣬���������ֻ����ܷ��ò�����![]() Ԫ��������Ͷ�ʹ�˾�������������ܷ�����ͣ���ͷ����Ƕ���.
Ԫ��������Ͷ�ʹ�˾�������������ܷ�����ͣ���ͷ����Ƕ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC����BAC��90����BC��5��AC��2![]() ����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
��1����BD�ij���
��2������AD�����DAC������ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com