
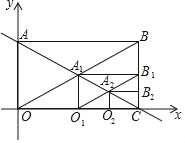
【题目】如图,直线y=![]() 与x轴y轴分别交于A、C两点,以AC为对角线作第一个矩形ABCO,对角线交点为A1,再以CA1为对角线作第二个矩形A1B1CO1,对角线交点为A2,同法作第三个矩形A2B2CO2对角线交点为A3,…以此类推,则第2019个矩形对角线交点A2019的坐标为_____.
与x轴y轴分别交于A、C两点,以AC为对角线作第一个矩形ABCO,对角线交点为A1,再以CA1为对角线作第二个矩形A1B1CO1,对角线交点为A2,同法作第三个矩形A2B2CO2对角线交点为A3,…以此类推,则第2019个矩形对角线交点A2019的坐标为_____.
【答案】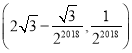
【解析】
根据矩形的性质,以及相似三角形的判定方法,可以证得:△AnCOn∽△ACO,相似比是![]() ,即可求得AnOn,OOn的长,进而得到An的坐标,据此可得点A2019的坐标.
,即可求得AnOn,OOn的长,进而得到An的坐标,据此可得点A2019的坐标.
解:在![]() 中,
中,
令x=0,解得:y=2;
令y=0,解得:x=2![]() ,
,
则OC=2![]() ,OA=2.
,OA=2.
∵A1是矩形ABCO的对角线的交点,O1A1∥OA,
∴△A1CO1∽△ACO,相似比是![]() ;
;
同理,△A2CO2∽△A1CO1,相似比是![]() ;
;
则△A2CO2∽△ACO,相似比是![]() =(
=(![]() )2,
)2,
同理:△AnCOn∽△ACO,相似比是(![]() )n.
)n.
∴![]() ,
,
∴AnOn=(![]() )nOA=(
)nOA=(![]() )n×2=(
)n×2=(![]() )n﹣1=
)n﹣1=![]() ,
,
COn=(![]() )n×OC=(
)n×OC=(![]() )n×2
)n×2![]() =(
=(![]() )n﹣1
)n﹣1![]() =
=![]() ,
,
OOn=2![]() ﹣
﹣![]() ,
,
则点An的坐标为(![]() ,
,![]() ),
),
∴点A2019的坐标为(![]() ,
,![]() ).
).
故答案为(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(2014湖南怀化)两个城镇A、B与两条公路ME、MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离相等,到两条公路ME、MF的距离也必须相等,且在∠FME的内部.
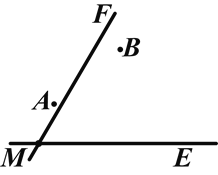
(1)那么点C应选在何处?请在图中,用尺规作图找出符合条件的点C(不写已知、求作、作法,只保留作图痕迹);
(2)设AB的垂直平分线交ME于点N,且![]() km,在M处测得点C位于点M的北偏东60°方向,在N处测得点C位于点N的北偏西45°方向,求点C到公路ME的距离.
km,在M处测得点C位于点M的北偏东60°方向,在N处测得点C位于点N的北偏西45°方向,求点C到公路ME的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x﹣a)(x+5)=x2﹣bx﹣5,一元二次方程ax2+bx+k=0的两个实数根x1,x2满足![]() (x1﹣x2)2﹣2x1x2=4,则k=_____.
(x1﹣x2)2﹣2x1x2=4,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
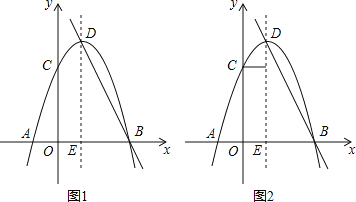
【题目】关于x的一元二次方程(m+1)x2+2(m+1)x+2=0有两个相等的实数根,抛物线y=﹣x2+(m+1)x+3与x轴交于A、B两点(A在B左侧),与y轴相交于点C,抛物线的顶点为D.
(1)求抛物线的解析式.
(2)如图1,设抛物线的对轴交x轴于点E,在抛物线的对称轴上是否存在点P,使P点到x轴的距离等于P点到直线BD的距离?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图2,作CF⊥DE于F,M为射线EA上一动点.如果在线段EF上恰好存在两个点N满足△CFN与△NEM相似,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现需了解2019年各月份中5至14日广州市每天最低气温的情况:图①是3月份的折线统计图.(数据来源于114天气网)
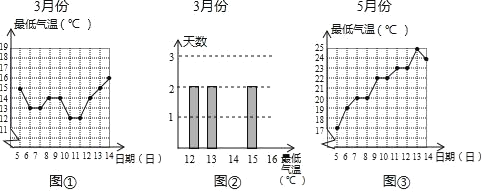
(1)图②是3月份的频数分布直方图,根据图①提供的信息,补全图②中的频数分布直方图;
(2)3月13日与10日这两天的最低气温之差是 ℃;
(3)图③是5月份的折线统计图.用![]() 表示5月份的方差;用
表示5月份的方差;用![]() 表示3月份的方差,比较大小:
表示3月份的方差,比较大小:![]()
![]() ;比较3月份与5月份, 月份的更稳定.
;比较3月份与5月份, 月份的更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
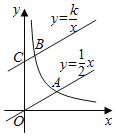
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为____.
x向上平移2个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
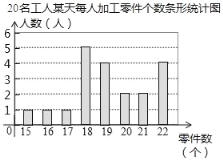
【题目】某部门为了解工人的生产能力情况,进行了抽样调查.该部门随机抽取了20名工人某天每人加工零件的个数,数据如下:整理上面数据,得到条形统计图;样本数据的平均数、众数、中位数如表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 19.2 | m | n |
根据以上信息,解答下列问题:
(1)上表中m、n的值分别为 , ;
(2)为调动积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让60%左右的工人能获奖,应根据 来确定奖励标准比较合适(填“平均数”、“众数”或“中位数”);
(3)该部门规定:每天加工零件的个数达到或超过21个的工人为生产能手若该部门有300名工人,试估计该部门生产能手的人数;
(4)现决定从小王、小张、小李、小刘中选两人参加业务能手比赛,直接写出恰好选中小张、小李两人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com