
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
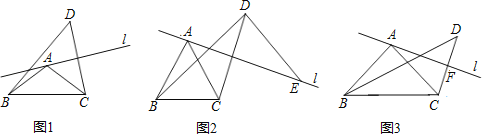
(1)如图1,
①求证:点B,C,D在以点A为圆心,AB为半径的圆上.
②直接写出∠BDC的度数(用含α的式子表示)为______.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD.
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转,当线段BF的长取得最大值时,直接写出tan∠FBC的值.
【答案】(1)①证明见解析;②![]() ;(2)证明见解析;(3)tan∠FBC=
;(2)证明见解析;(3)tan∠FBC=![]() .
.
【解析】
(1)①由线段垂直平分线的性质可得AD=AC=AB,即可证点B,C,D在以点A为圆心,AB为半径的圆上;
②由圆周角定理可得∠BAC=2∠BDC,可求∠BDC的度数;
(2)连接CE,由题意可证△ABC,△DCE是等边三角形,可得AC=BC,∠DCE=60°=∠ACB,CD=CE,根据“SAS”可证△BCD≌△ACE,可得AE=BD;
(3)取AC的中点O,连接OB,OF,BF,由三角形的三边关系可得,当点O,点B,点F三点共线时,BF最长,根据等腰三角形的性质和勾股定理可求,OH=HC,BH=3HC,即可求tan∠FBC的值.
证明:(1)①如图1,连接DA,

∵点C关于直线l的对称点为点D,
∴AD=AC,且AB=AC,
∴AD=AB=AC,
∴点B,C,D在以点A为圆心,AB为半径的圆上;
②∵点B,C,D在以点A为圆心,AB为半径的圆上,
∴∠BDC=![]() ;
;
(2)如图2,连接CE,
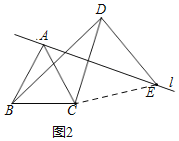
∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形,
∴BC=AC,∠ACB=60°,
∵∠BDC=![]() ,
,
∴∠BDC=30°,
∵BD⊥DE,
∴∠CDE=60°,
∵点C关于直线l的对称点为点D,
∴DE=CE,且∠CDE=60°,
∴△CDE是等边三角形,
∴CD=CE=DE,∠DCE=60°=∠ACB,
∴∠BCD=∠ACE,且AC=BC,CD=CE,
∴△BCD≌△ACE(SAS),
∴BD=AE;
(3)如图3,取AC的中点O,连接OB,OF,BF,
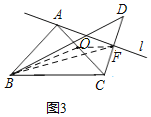
∵在△BOF中,BO+OF≥BC,
∴当点O,点B,点F三点共线时,BF最长,
如图,过点O作OH⊥BC,
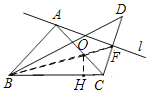
∵∠BAC=90°,AB=AC,
∴BC=![]() AC,∠ACB=45°,
AC,∠ACB=45°,
∴∠COH=∠HCO=45°,
∴OH=HC,
∴OC=![]() HC,
HC,
∵点O是AC中点,
∴AC=2
∴BC=4HC,
∴BH=BC﹣HC=3HC,
∴tan∠FBC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
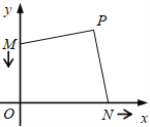
【题目】如图,动点![]() 从(0,3)出发,沿
从(0,3)出发,沿![]() 轴以每秒1个单位长度的速度向下移动,同时动点
轴以每秒1个单位长度的速度向下移动,同时动点![]() 从
从![]() 出发,沿
出发,沿![]() 轴以每秒2个单位长度的速度向右移动,当点
轴以每秒2个单位长度的速度向右移动,当点![]() 移动到
移动到![]() 点时,点
点时,点![]() 、
、![]() 同时停止移动.点
同时停止移动.点![]() 在第一象限内,在
在第一象限内,在![]() 、
、![]() 移动过程中,始终有
移动过程中,始终有![]() ,且
,且![]() .则在整个移动过程中,点
.则在整个移动过程中,点![]() 移动的路径长为( )
移动的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
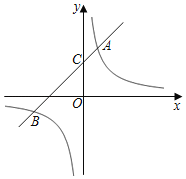
【题目】如图,在平面直角坐标系内xOy中,某一次函数的图象与反比例函数的y=![]() 的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
(1)求该一次函数的解析式;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
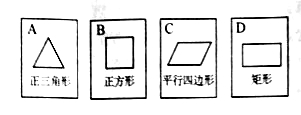
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进校时需要从学校大门A、B、C三个入口处中的任意一处测量体温,体温正常方可进校.
(1)甲同学在A入口处测量体温的概率是 ;
(2)求甲、乙两位同学在同一入口处测量体温的概率.(用“画树状图”或“列表”的方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
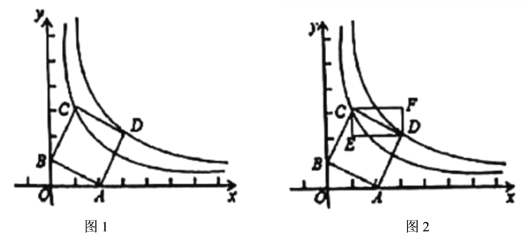
【题目】如图1,在平面直角坐标系中点![]() ,
,![]() ,以
,以![]() 为顶点在第一象限内作正方形
为顶点在第一象限内作正方形![]() .反比例函数
.反比例函数![]() 、
、![]() 分别经过
分别经过![]() 、
、![]() 两点(1)如图2,过
两点(1)如图2,过![]() 、
、![]() 两点分别作
两点分别作![]() 、
、![]() 轴的平行线得矩形
轴的平行线得矩形![]() ,现将点
,现将点![]() 沿
沿![]() 的图象向右运动,矩形
的图象向右运动,矩形![]() 随之平移;
随之平移;
①试求当点![]() 落在
落在![]() 的图象上时点
的图象上时点![]() 的坐标_____________.
的坐标_____________.
②设平移后点![]() 的横坐标为
的横坐标为![]() ,矩形的边
,矩形的边![]() 与
与![]() ,
,![]() 的图象均无公共点,请直接写出
的图象均无公共点,请直接写出![]() 的取值范围____________.
的取值范围____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com