
分析 (1)根据幂的乘方和同底数幂的乘法进行计算即可;
(2)根据同底数幂的乘法进行计算即可;
(3)根据幂的乘方和同底数幂的乘法进行计算即可;
(4)根据幂的乘方和同底数幂的乘法进行计算即可;
(5)根据同底数幂的除法进行计算即可;
(6)先根据积的乘方和幂的乘方进行计算,再计算单项式的除法即可;
(7)根据除以一个数等于乘积这个数的倒数转化为乘法,再按照乘法的分配律进行计算即可;
(8)根据负整数指数幂、绝对值、乘法进行计算即可.
解答 解:(1)原式=a3m•an,
=a3m+n;
(2)原式=t3•t4•t5
=t12;
(3)原式=a6+a6-a6
=a6,
)(-2a2)2•a4-(-5a4)2
(4)原式=4a4•a4-25a8
=4a8-25a8
=-21a8;
(5)原式=(a-b)10÷(a-b)4÷(a-b)3
=(a-b)3;
(6)原式=-x10y5÷(-x6y3)
=x4y2;
(7)原式=($\frac{3}{4}$+$\frac{5}{6}$-$\frac{7}{12}$)×24
=18+20-14
=24;
(8)原式=-1-5+2
=-4.
点评 本题考查了单项式乘以多项式、积的乘方和幂的乘方、完全平方公式的运用,熟记运算法则是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
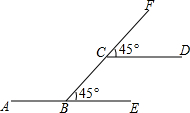 如图所示,一辆汽车在笔直的公路上行驶.第一次向左拐45°,再在笔直的公路上行驶一段距离后,第二次向右拐45°,请判断这辆汽车行驶的方向是否和原来的方向相同?为什么?
如图所示,一辆汽车在笔直的公路上行驶.第一次向左拐45°,再在笔直的公路上行驶一段距离后,第二次向右拐45°,请判断这辆汽车行驶的方向是否和原来的方向相同?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 太阳从西方升起 | |
| B. | 若a<0,则|a|=-a | |
| C. | 打开电视正在播放动画片《喜羊羊与灰太狼》 | |
| D. | 某运动员投篮时连续3次全中 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com