
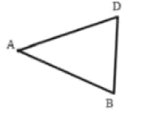
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.

(1)画图:平移三角形ABC至三角形![]() ,使点A与A对应.
,使点A与A对应.
(2)线段AB与![]() 的位置关系是________.
的位置关系是________.
(3)求![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】2019年5月26日振奋人心的“数博会”在我省贵阳市隆重召开。某校组织部分师生前往参观学习,租用A、B两种型号的旅游车共8辆。一辆A型车可坐40人,一辆B型车可坐35人。
(1)若前往参观的师生共310人,为了刚好将全部师生送达目的地,应分别租用A、B两种型号的旅游车各多少辆?
(2)若A型号的车每辆租金需220元,B型号的车每辆租金需160元,学校要求总租车费用不超过1540元,那么最多可租用多少辆A型号的旅游车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小欣设计的“利用等腰三角形做菱形”的尺规作图过程.
己知:等腰![]()
求作:点![]() ,使得四边形
,使得四边形![]() 为菱形.
为菱形.
做法:①作![]() 的角平分线
的角平分线![]() ,交线段
,交线段![]() 于点
于点![]() ;
;
②以点![]() 为圆心,
为圆心,![]() 长为半径圆弧,交
长为半径圆弧,交![]() 的延长线于点
的延长线于点![]() ;
;
③连接![]() ,所以四边形
,所以四边形![]() 为菱形,点
为菱形,点![]() 即为所求.
即为所求.
根据小新设计的尺规作图过程.
(1)使用直尺和圆规补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:![]() 平分
平分![]() ,
,
![]() (______________________________________)(填推理的依据)
(______________________________________)(填推理的依据)
![]()
∴四边形![]() 为平行四边形(______________________________________)(填推理的依据)
为平行四边形(______________________________________)(填推理的依据)
![]() ,
,
∴四边形![]() 为菱形(______________________________________)(填推理的依据)
为菱形(______________________________________)(填推理的依据)
(3)请你设计一种不同于小欣的,利用等腰![]() (其中
(其中![]() )作菱形
)作菱形![]() 的方法.
的方法.
要求:写出简要思路,并尺规作图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )

A. △ABC中,AD是边BC上的高
B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高
D. △GBC中,CF是边BG上的高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上![]() 点、
点、![]() 点表示的数为
点表示的数为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ;线段
;线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .已知数轴上有
.已知数轴上有![]() 、
、![]() 两点,分别表示的数为
两点,分别表示的数为![]() 和
和![]() ,点
,点![]() 以每秒
以每秒![]() 个单位的速度沿数轴向右匀速运动,点
个单位的速度沿数轴向右匀速运动,点![]() 以每秒
以每秒![]() 个单位向左匀速运动.设运动时间为
个单位向左匀速运动.设运动时间为![]() 秒(
秒(![]() )
)
(![]() )运动开始前,
)运动开始前,![]() 、
、![]() 两点的距离为__________;线段
两点的距离为__________;线段![]() 的中点
的中点![]() 所表示的数为__________.
所表示的数为__________.
(![]() )它们按上述方式运动,
)它们按上述方式运动,![]() 、
、![]() 两点两点经过多少秒会相遇,相遇点所表示的数是什么?
两点两点经过多少秒会相遇,相遇点所表示的数是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )

A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在一个盒子旦有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频率 | 17 | 32 | 44 | 64 | 78 | a | 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 | b | 0.302 | c |
(1)请将表格中的数据补齐a= ;b= ;c= ;
(2)根据上表,完成折线统计图;

当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1)
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=k1x(k1≠0)与反比例函数![]() 的图象交于A、B两点,点A的坐标为(2,1).
的图象交于A、B两点,点A的坐标为(2,1).
(1)求正比例函数、反比例函数的表达式;
(2)求点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com