
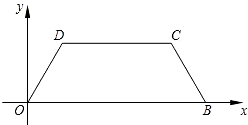
 ЙдПЯMD1Ҫ»ұЯDCУЪөгEЈ¬ЙдПЯMC1Ҫ»ұЯCBУЪөгFЈ¬ЙиDE=mЈ¬BF=nЈ®ЗуmУлnөДәҜКэ№ШПөКҪЈ®
ЙдПЯMD1Ҫ»ұЯDCУЪөгEЈ¬ЙдПЯMC1Ҫ»ұЯCBУЪөгFЈ¬ЙиDE=mЈ¬BF=nЈ®ЗуmУлnөДәҜКэ№ШПөКҪЈ®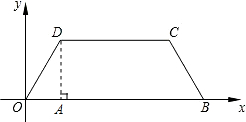 ҪвЈәЈЁ1Ј©№эөгDЧчDAЎНOBЈ¬ҙ№ЧгОӘAЈ®
ҪвЈәЈЁ1Ј©№эөгDЧчDAЎНOBЈ¬ҙ№ЧгОӘAЈ® Ј¬
Ј¬ Ј©Ј¬
Ј©Ј¬ Ј©Ј¬өГ
Ј©Ј¬өГ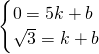 Ј¬
Ј¬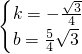 Ј¬
Ј¬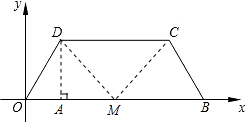
 x+
x+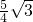 Ј»
Ј»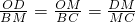 Ј¬
Ј¬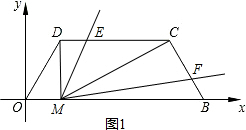 OM=1Ј¬BM=4Ј®
OM=1Ј¬BM=4Ј®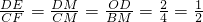 Ј¬
Ј¬ Ј»
Ј»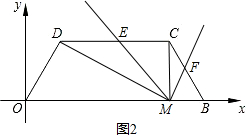 OM=4Ј¬BM=1Ј®
OM=4Ј¬BM=1Ј®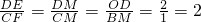 Ј¬
Ј¬ »тm=4-2nЈ®
»тm=4-2nЈ® Ј©Ј¬ЙиЦұПЯDBөДәҜКэұнҙпКҪОӘy=kx+bЈ¬°СөгBЈЁ5Ј¬0Ј©Ј¬DЈЁ1Ј¬
Ј©Ј¬ЙиЦұПЯDBөДәҜКэұнҙпКҪОӘy=kx+bЈ¬°СөгBЈЁ5Ј¬0Ј©Ј¬DЈЁ1Ј¬ Ј©ҙъИлҪвОцКҪАыУГҙэ¶ЁПөКэ·ЁЈ¬өГЦұПЯDBөДәҜКэұнҙпКҪОӘy=-
Ј©ҙъИлҪвОцКҪАыУГҙэ¶ЁПөКэ·ЁЈ¬өГЦұПЯDBөДәҜКэұнҙпКҪОӘy=- x+
x+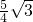 Ј»
Ј»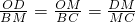 Ј¬ЛщТФOD•BC=BM•OMЈ®ЙиOM=xЈ¬ФтBM=5-xЈ¬өГ2ЎБ2=xЈЁ5-xЈ©Ј¬ҪвөГxөДЦөЈ¬јҙҝЙЗуөГMөгЧшұкЈ»
Ј¬ЛщТФOD•BC=BM•OMЈ®ЙиOM=xЈ¬ФтBM=5-xЈ¬өГ2ЎБ2=xЈЁ5-xЈ©Ј¬ҪвөГxөДЦөЈ¬јҙҝЙЗуөГMөгЧшұкЈ»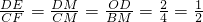 Ј¬
Ј¬ Ј®ЈЁўтЈ©өұMөгЧшұкОӘЈЁ4Ј¬0Ј©КұЈ¬OM=4Ј¬BM=1Ј®Н¬ЈЁўсЈ©Ј¬ҝЙөГЎчDMEЎЧЎчCMFЈ¬өГ
Ј®ЈЁўтЈ©өұMөгЧшұкОӘЈЁ4Ј¬0Ј©КұЈ¬OM=4Ј¬BM=1Ј®Н¬ЈЁўсЈ©Ј¬ҝЙөГЎчDMEЎЧЎчCMFЈ¬өГ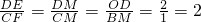 Ј¬ЛщТФDE=2CFЈ®ҪвөГm=2ЈЁ2-nЈ©Ј¬јҙm=4-2nЈ®
Ј¬ЛщТФDE=2CFЈ®ҪвөГm=2ЈЁ2-nЈ©Ј¬јҙm=4-2nЈ®


| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкЦРЈ¬ЛДұЯРОOABCКЗөИСьМЭРОЈ¬CBЎОOAЈ¬OA=7Ј¬AB=4Ј¬ЎПCOA=60ЎгЈ¬өгPОӘxЦбЙПөДТ»ёц¶ҜөгЈ¬ө«КЗөгPІ»Улөг0ЎўөгAЦШәПЈ®Б¬ҪУCPЈ¬DөгКЗПЯ¶ОABЙПТ»өгЈ¬Б¬ҪУPDЈ®
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкЦРЈ¬ЛДұЯРОOABCКЗөИСьМЭРОЈ¬CBЎОOAЈ¬OA=7Ј¬AB=4Ј¬ЎПCOA=60ЎгЈ¬өгPОӘxЦбЙПөДТ»ёц¶ҜөгЈ¬ө«КЗөгPІ»Улөг0ЎўөгAЦШәПЈ®Б¬ҪУCPЈ¬DөгКЗПЯ¶ОABЙПТ»өгЈ¬Б¬ҪУPDЈ®| BD |
| AB |
| 5 |
| 8 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
 ЈЁ2012•УеұұЗшТ»ДЈЈ©ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкxoyЦРЈ¬ТФЧшұкФӯөгOОӘФІРДЈ¬3ОӘ°лҫ¶»ӯФІЈ¬ҙУҙЛФІДЪЈЁ°ьАЁұЯҪзЈ©өДЛщУРХыКэөгЈЁәбЎўЧЭЧшұкҫщОӘХыКэЈ©ЦРИОТвСЎИЎТ»ёцөгЈ¬ЖдәбЎўЧЭЧшұкЦ®әНОӘ0өДёЕВККЗ
ЈЁ2012•УеұұЗшТ»ДЈЈ©ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкxoyЦРЈ¬ТФЧшұкФӯөгOОӘФІРДЈ¬3ОӘ°лҫ¶»ӯФІЈ¬ҙУҙЛФІДЪЈЁ°ьАЁұЯҪзЈ©өДЛщУРХыКэөгЈЁәбЎўЧЭЧшұкҫщОӘХыКэЈ©ЦРИОТвСЎИЎТ»ёцөгЈ¬ЖдәбЎўЧЭЧшұкЦ®әНОӘ0өДёЕВККЗ| 5 |
| 29 |
| 5 |
| 29 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкЦРЈ¬өИСьМЭРОABCDөДПВөЧФЪxЦбЙПЈ¬ЗТBөгЧшұкОӘЈЁ4Ј¬0Ј©Ј¬DөгЧшұкОӘЈЁ0Ј¬3Ј©Ј¬ФтACіӨОӘ
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкЦРЈ¬өИСьМЭРОABCDөДПВөЧФЪxЦбЙПЈ¬ЗТBөгЧшұкОӘЈЁ4Ј¬0Ј©Ј¬DөгЧшұкОӘЈЁ0Ј¬3Ј©Ј¬ФтACіӨОӘІйҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкxOyЦРЈ¬ТСЦӘөгAЈЁ-5Ј¬0Ј©Ј¬PКЗ·ҙұИАэәҜКэy=
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкxOyЦРЈ¬ТСЦӘөгAЈЁ-5Ј¬0Ј©Ј¬PКЗ·ҙұИАэәҜКэy=| k |
| x |
| k |
| x |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
 ЎПCOA=45ЎгЈ¬¶ҜөгPҙУөгOіц·ўЈ¬ФЪМЭРОOABCөДұЯЙПФЛ¶ҜЈ¬В·ҫ¶ОӘOЎъAЎъBЎъCЈ¬өҪҙпөгCКұНЈЦ№Ј®ЧчЦұПЯCPЈ®
ЎПCOA=45ЎгЈ¬¶ҜөгPҙУөгOіц·ўЈ¬ФЪМЭРОOABCөДұЯЙПФЛ¶ҜЈ¬В·ҫ¶ОӘOЎъAЎъBЎъCЈ¬өҪҙпөгCКұНЈЦ№Ј®ЧчЦұПЯCPЈ®Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com