
【题目】如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO. 
(1)求证:△CDP≌△POB;
(2)填空: ①若AB=4,则四边形AOPD的最大面积为;
②连接OD,当∠PBA的度数为时,四边形BPDO是菱形.
【答案】
(1)证明:∵PC=PB,D是AC的中点,
∴DP∥AB,
∴DP= ![]() AB,∠CPD=∠PBO,
AB,∠CPD=∠PBO,
∵BO= ![]() AB,
AB,
∴DP=BO,
在△CDP与△POB中,

∴△CDP≌△POB(SAS);
(2)4;60°
【解析】(2)解:①当四边形AOPD的AO边上的高等于半径时有最大面积, (4÷2)×(4÷2)
=2×2
=4;②如图: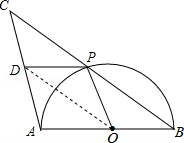
∵DP∥AB,DP=BO,
∴四边形BPDO是平行四边形,
∵四边形BPDO是菱形,
∴PB=BO,
∵PO=BO,
∴PB=BO=PO,
∴△PBO是等边三角形,
∴∠PBA的度数为60°.
故答案为:4;60°.
(1)根据中位线的性质得到DP∥AB,DP= ![]() AB,由SAS可证△CDP≌△POB;(2)①当四边形AOPD的AO边上的高等于半径时有最大面积,依此即可求解;②根据有一组对应边平行且相等的四边形是平行四边形,可得四边形BPDO是平行四边形,再根据邻边相等的平行四边形是菱形,以及等边三角形的判定和性质即可求解.
AB,由SAS可证△CDP≌△POB;(2)①当四边形AOPD的AO边上的高等于半径时有最大面积,依此即可求解;②根据有一组对应边平行且相等的四边形是平行四边形,可得四边形BPDO是平行四边形,再根据邻边相等的平行四边形是菱形,以及等边三角形的判定和性质即可求解.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】我市某中学八年级一班准备在“七一”组织参加红色旅游,班长把全班48名同学对旅游地点的意向绘制成了扇形统计图,其中“想去我市龙州县红八军纪念馆参加的学生数”的扇形圆心角为60°,则下列说法中正确的是( )
A.想去龙州县红八军纪念馆参加的学生占全班学生的60%
B.想去龙州县红八军纪念馆参观的学生有12人
C.想去龙州县红八军纪念馆参观的学生肯定最多
D.想去龙州县红八军纪念馆参观的学生占全班学生的 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E. 
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)问题发现:
如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC,请判断:FG与CE的数量关系是 , 位置关系是 . 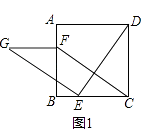
(2)拓展探究:
如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;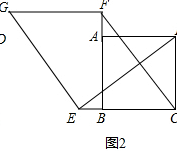
(3)类比延伸:
如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.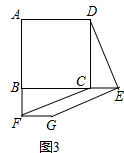
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F. 
(1)求证:AB=AC;
(2)若AD=2 ![]() ,∠DAC=30°,求AC的长.
,∠DAC=30°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,矩形ABCD关于y轴对称,点A,D在x轴上,BC交y轴于点F,E是OF的中点,抛物线y=ax2+bx+c经过B,E,C三点,已知点B(﹣2,﹣2),解答下列问题: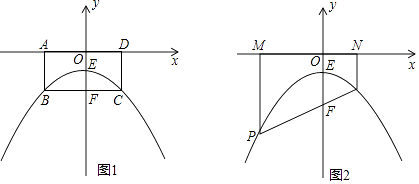
(1)填空:a= , b= , c= .
(2)如图2,这P是上述抛物线上一点,连接PF并延长交抛物线于另外一点Q,PM⊥x轴于M,QN⊥x轴于N.
①求证:PM+QN=PQ;
②若PQ=m,S四边形PMNQ= ![]() m2 , 求直线PQ对应的一次函数的解析式.
m2 , 求直线PQ对应的一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com