练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，平行四边形的两个顶点在反比例函数的图象上，点在轴上，且两点关于原点对称，交轴于点，已知点的坐标是（2，3）．

    （1）求的值；

    （2）若的面积为2，求点的坐标．

    【答案】（1）6 （2）(-4，0)

    【解析】

    （1）将点的坐标是（2，3）代入反比例函数解析式即可得出k的值；

    （2）设点P的坐标为(0，m)，直线AP的解析式为，依据三角形面积得出m的值，再根据A，P的坐标求出直线AP的解析式，即可求出点D的坐标．

    解：（1）∵点A(2，3)在反比例函数的图象上，

    ∴ ；

    （2）设点P的坐标为(0，m)，直线AP的解析式为

    依题意得

    解得，即点P的坐标为(0，2)．

    则解得，因此直线AP的解析式为

    ∵点D在直线AP上，∴，解得

    ∴D点的坐标为(-4，0)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

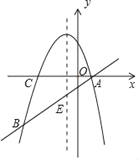
    【题目】如图，抛物线y＝ax2+bx+3(a≠0)的对称轴为直线x＝﹣1，抛物线交x轴于A、C两点，与直线y＝x﹣1交于A、B两点，直线AB与抛物线的对称轴交于点E．

    (1)求抛物线的解板式．

    (2)点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标．

    (3)在平面直角坐标系中，以点B、E、C、D为顶点的四边形是平行四边形，请直接写出符合条件点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′．若∠CC′B′＝32°，则∠B的大小是（ ）

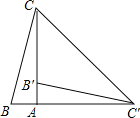
    A.32°B.64°C.77°D.87°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在 ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S四边形DEBC=2S△EFB；④∠CFE=3∠DEF,其中正确结论的个数共有（ ）.

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2．

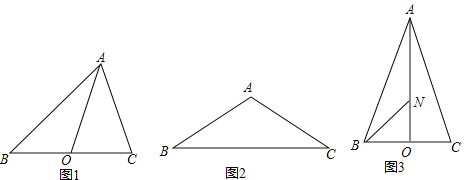
    （1）在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC= ，OC△OA= ；

    （2）如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；

    （3）如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON=AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

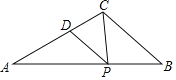
    【题目】如图，在△ABC中，AB＝6，AC＝4，∠A＝30°，线段AB上有一个动点P，过点P作PD∥BC，交AC于D，连接PC，则△PCD的最大面积是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

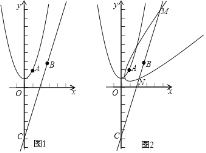
    【题目】如图1，已知抛物线的顶点坐标为（0，1）且经过点A（1，2），直线y＝3x﹣4经过点B（，n），与y轴交点为C．

    （1）求抛物线的解析式及n的值；

    （2）将直线BC绕原点O逆时针旋转45°，求旋转后的直线的解析式；

    （3）如图2将抛物线绕原点O顺时针旋转45°得到新曲线，新曲线与直线BC交于点M、N，点M在点N的上方，求点N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

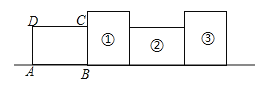
    【题目】如图，将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置，继续绕右下角的顶点按顺时针方向旋转90°至图②位置，以此类推，这样连续旋转2017次．若AB=4，AD=3，则顶点A在整个旋转过程中所经过的路径总长为（ ）

    A. 2017π B. 2034π C. 3024π D. 3026π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，矩形ABCD中，过对角线BD中点O的直线分别交AB，CD边于点E、F．

    （1）求证：四边形BEDF是平行四边形；

    （2）只需添加一个条件，即______，可使四边形BEDF为菱形．

    查看答案和解析>>

    同步练习册答案