
����Ŀ�����ǹ涨���������������ߵġ�����ֵ�����ڵ������ϵ����ߺ����һ���ƽ�����ͼ1���ڡ�ABC�У�AO��BC���ϵ����ߣ�AB��AC�ġ�����ֵ���͵���AO2��BO2��ֵ���ɼ�ΪAB��AC=AO2��BO2��
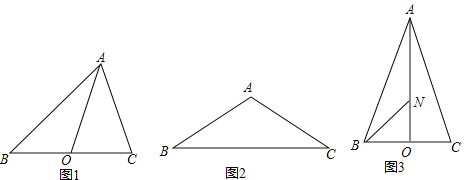
��1����ͼ1�У�����BAC=90�㣬AB=8��AC=6��AO��BC���ϵ����ߣ���AB��AC= ��OC��OA= ��
��2����ͼ2���ڡ�ABC�У�AB=AC=4����BAC=120�㣬��AB��AC��BA��BC��ֵ��
��3����ͼ3���ڡ�ABC�У�AB=AC��AO��BC���ϵ����ߣ���N��AO�ϣ���ON=![]() AO����֪AB��AC=14��BN��BA=10�����ABC�������
AO����֪AB��AC=14��BN��BA=10�����ABC�������
���𰸡���1��0��7����2����8��24����3��![]() ��
��
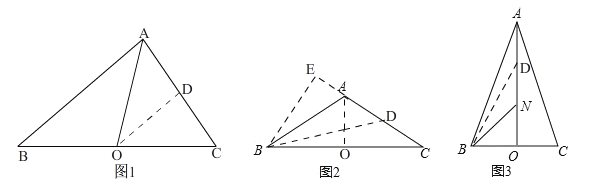
�������������������1�����ȸ��ݹ��ɶ������BC=10��������ֱ�������ε����ʵó�OA=OB=OC=5����������¶��弴�ɵó����ۣ�
�����õ��������ε��������CD=3�������ù��ɶ������OD��������¶��弴�ɵó����ۣ�
��2���������ú�30���ֱ�������ε��������AO=2��OB=![]() �������¶��弴�ɵó����ۣ�
�������¶��弴�ɵó����ۣ�
���ȹ���ֱ�����������BE��AE�����ù��ɶ������BD��������¶��弴�ɵó����ۣ�
��3���ȹ���ֱ�������Σ�������OA��BD2��������¶��彨����������⼴�ɵó����ۣ�
�����������1���١ߡ�BAC=90�㣬AB=8��AC=6����BC=10��
�ߵ�O��BC���е㣬��OA=OB=OC=![]() BC=5����AB��AC=AO2��BO2=25��25=0��
BC=5����AB��AC=AO2��BO2=25��25=0��
����ͼ1��ȡAC���е�D������OD����CD=![]() AC=3��
AC=3��
��OA=OC=5����OD��AC��
��Rt��COD��OD=![]() =4����OC��OA=OD2��CD2=16��9=7��
=4����OC��OA=OD2��CD2=16��9=7��
�ʴ�Ϊ��0��7��
��2������ͼ2��ȡBC���е�D������AO����AB=AC����AO��BC��
�ڡ�ABC�У�AB=AC����BAC=120�㣬���ABC=30�㣬
��Rt��AOB�У�AB=4����ABC=30�㣬��AO=2��OB=![]() ��
��
��AB��AC=AO2��BO2=4��12=��8��
��ȡAC���е�D������BD����AD=CD=![]() AC=2������B��BE��AC��CA���ӳ�����E����Rt��ABE�У���BAE=180�㩁��BAC=60�㣬���ABE=30�㣬
AC=2������B��BE��AC��CA���ӳ�����E����Rt��ABE�У���BAE=180�㩁��BAC=60�㣬���ABE=30�㣬
��AB=4����AE=2��BE=![]() ����DE=AD+AE=4��
����DE=AD+AE=4��
��Rt��BED�У����ݹ��ɶ����ã�BD=![]() =
=![]() =
=![]() ��
��
��BA��BC=BD2��CD2=24��
��3����ͼ3����ON=x��OB=OC=y����BC=2y��OA=3x��
��AB��AC=14����OA2��OB2=14����9x2��y2=14�٣�
ȡAN���е�D������BD����AD=DB=![]() AN=
AN=![]() ��
��![]() OA=ON=x����OD=ON+DN=2x��
OA=ON=x����OD=ON+DN=2x��
��Rt��BOD��BD2=OB2+OD2=y2+4x2����BN��BA=10��
��BD2��DN2=10����y2+4x2��x2=10����3x2+y2=10��
�����٢ڵã� 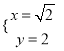 ��
��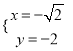 ���ᣩ����BC=4��OA=
���ᣩ����BC=4��OA=![]() ����S��ABC=
����S��ABC=![]() BC��AO=
BC��AO=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
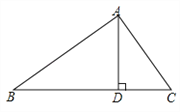
����Ŀ����ͼ����ABC�У���BAC��90�㣬AD��BC������ΪD��
��1��������ABC��ƽ���ߣ��ֱ�AD��AC��P��Q���㣻��Ҫ�߹���ͼ��������ͼ�ۼ�����д������
��2��֤��AP��AQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ�����AD�ڵ�E����BA���ӳ����ڵ�F��

��1����֤����APD�ա�CPD��
��2����֤����APE�ס�FPA��
��3����PE��2��EF��6����PC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ������������ijˮ���깺��һ����ˮ��������Ϊ20Ԫ/ǧ�ˣ��ۼ۲�����20Ԫ/ǧ�ˣ��Ҳ�����32Ԫ/ǧ�ˣ�����������������ָ�ˮ��һ���������y��ǧ�ˣ��������ۼ�x��Ԫ/ǧ�ˣ��������±���ʾ��һ�κ�����ϵ��
������y��ǧ�ˣ� | �� | 34.8 | 32 | 29.6 | 28 | �� |
�ۼ�x��Ԫ/ǧ�ˣ� | �� | 22.6 | 24 | 25.2 | 26 | �� |
��1��ij������ˮ�����ۼ�Ϊ23.5Ԫ/ǧ�ˣ������ˮ������������
��2�����ij����������ˮ������150Ԫ����ô����ˮ�����ۼ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��tan��ACB=2��D�ڡ�ABC�ڲ�����AD=CD����ADC=90��������BD������BCD�����Ϊ10����AD�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���![]() ����������
����������![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ���
��ͼ���ϣ���![]() ��
��![]() ���ϣ���
���ϣ���![]() �������ԭ��Գƣ�
�������ԭ��Գƣ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����֪��
����֪��![]() �������ǣ�2��3����
�������ǣ�2��3����

��1����![]() ��ֵ��
��ֵ��
��2����![]() �����Ϊ2����
�����Ϊ2����![]() ������꣮
������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ�����֪ʶ���������㹺��A��B���ֽ�Ʒ���������A��Ʒ10����B��Ʒ5��������120Ԫ���������A��Ʒ5����B��Ʒ10��������90Ԫ��
��1��A��B���ֽ�Ʒÿ��������Ԫ��
��2��������A��B��Ʒ��100�����ܷ��ò�����600Ԫ����A��Ʒ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Уѧ���ᷢ��ͬѧ�ǾͲ�ʱʣ��˽϶࣬�˷����أ���������У�ڳ����������ж�������ͬѧ����ϧ��ʳ��Ϊ����ͬѧ��������λ����Ҫ�ԣ�Уѧ������ij����ͺ���������˲���ͬѧ�Ͳͷ��˵�ʣ��������������ͳ�ƺ���Ƴ�����ͼ��ʾ�IJ�������ͳ��ͼ��
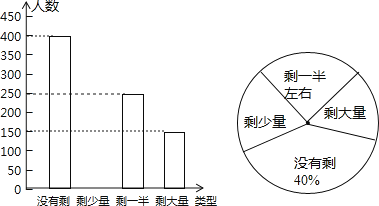
��1����α������ͬѧ������ ������
��2����ȫ����ͳ��ͼ��
��3������������ͳ��ͼ��ʣ������������Ӧ����Բ�ĽǵĶ�����
��4��Уѧ����ͨ�����ݷ�����������α����������ѧ��һ���˷ѵ�ʳ����Թ�200����һ�ͣ��ݴ˹��㣬��У20000��ѧ��һ���˷ѵ�ʳ��ɹ�������ʳ��һ�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
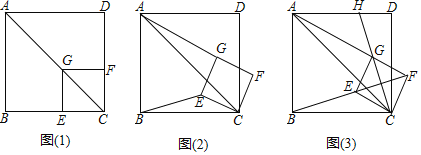
����Ŀ����ͼ��1������֪��G��������ABCD�ĶԽ���AC�ϣ�GE��BC��GF��CD��
��1������֤���ı���CEGF�������Σ����ƶϣ�![]() ��ֵΪ������
��ֵΪ������
��2����������CEGF�Ƶ�C˳ʱ�뷽����ת���ǣ�0��������45��������ͼ��2����ʾ����̽���߶�AG��BE֮���������ϵ��
��3��������CEGF����ת�����У���B��E��F������һ��ֱ����ʱ����ͼ��3����ʾ���ӳ�CG��AD�ڵ�H����AG��6��GH��2![]() ����������CEGF��������ABCD�ı߳���
����������CEGF��������ABCD�ı߳���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com