
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,GF⊥CD.
(1)①求证:四边形CEGF是正方形;②推断:![]() 的值为 :
的值为 :
(2)将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系;
(3)正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,求正方形CEGF和正方形ABCD的边长.
,求正方形CEGF和正方形ABCD的边长.
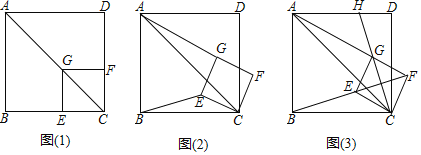
【答案】(1)![]() ;(2)AG=
;(2)AG=![]() BE;(3)正方形CEGF的边长为3,正方形ABCD的边长为3
BE;(3)正方形CEGF的边长为3,正方形ABCD的边长为3![]() .
.
【解析】
(1)①由GE⊥BC、GF⊥CD结合得∠BCD=90°,可得四边形CEGF是矩形,再由∠ECG=45°即可得证;
②由正方形性质知∠CEG=∠B=90°、∠ECG=45°,据此可得![]() =
=![]() 、GE∥AB,利用平行线分线段成比例定理可得;
、GE∥AB,利用平行线分线段成比例定理可得;
(2)连接CG,只需证△ACG∽△BCE即可得;
(3)证△AHG∽△CHA得![]() =
=![]() ,设BC=CD=AD=a,知AC=
,设BC=CD=AD=a,知AC=![]() a,则由
a,则由![]() ,得
,得![]() ,计算AH=
,计算AH=![]() ,代入可得:a=3
,代入可得:a=3![]() ,可得结论.
,可得结论.
解:(1)①如图(1),∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴![]() =
=![]() ,GE∥AB,
,GE∥AB,
∴![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)连接CG,
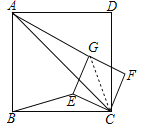
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,![]() =cos45°=
=cos45°=![]() ,
,![]() =cos45°=
=cos45°=![]() ,
,
∴![]() =
=![]() ,
,
∴△ACG∽△BCE,
∴![]() =
=![]() ,
,
∴线段AG与BE之间的数量关系为AG=![]() BE;
BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴![]() =
=![]() ,
,
设BC=CD=AD=a,则AC=![]() a,
a,
则由![]() ,得
,得![]()
∴AH=![]() ,
,
则DH=AD﹣AH=![]() a,CH=
a,CH=![]() =
=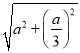 =
=![]() ,
,
∴![]() 得
得![]() =
=![]() ,
,
解得:a=3![]() ,即BC=3
,即BC=3![]() ,CH=
,CH=![]() ×
×![]() =5
=5![]() ,
,
∴CG=CH﹣GH=5![]() ﹣2
﹣2![]() =3
=3![]() ,
,
∵四边形CEGF是正方形,
∴CF=3,
综上,正方形CEGF的边长为3,正方形ABCD的边长为3![]() .
.


科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2.
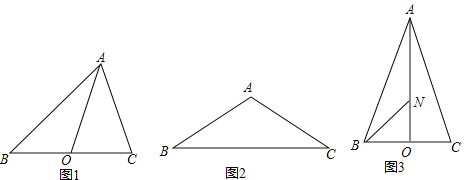
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= ,OC△OA= ;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
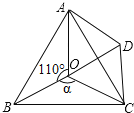
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当△AOD是直角三角形且∠ADO=90°时,求α的度数;
(3)当α=110°或125°或140°时,判断△AOD的形状,请选择其中一种情况说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
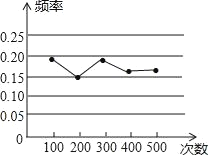
A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,矩形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)只需添加一个条件,即______,可使四边形BEDF为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任一点,PQ⊥BC于Q,PR⊥BE于R.有下列结论:①△PCQ∽△PER;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论的个数是( )
.其中正确的结论的个数是( )
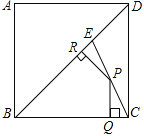
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
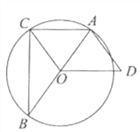
【题目】如图,已知△ABC内接于![]() ,AB是直径,OD∥AC,AD=OC.
,AB是直径,OD∥AC,AD=OC.
(1)求证:四边形OCAD是平行四边形;
(2)填空:①当∠B= 时,四边形OCAD是菱形;
②当∠B= 时,AD与![]() 相切.
相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com