
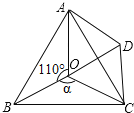
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当△AOD是直角三角形且∠ADO=90°时,求α的度数;
(3)当α=110°或125°或140°时,判断△AOD的形状,请选择其中一种情况说明理由.
【答案】(1)证明见解析;(2)150°;(3)△AOD是等腰三角形,证明见解析
【解析】
(1)根据等边三角形的性质可得∠ACB=60°,然后根据旋转的性质可得∠OCB=∠DCA,OC=DC,即可证出∠ACB=∠OCD=60°,从而证出结论;
(2)根据等边三角形的性质和已知条件即可求出∠ADC,然后根据旋转的性质即可求出结论;
(3)根据α的度数、旋转的性质、周角的定义、三角形的内角和定理分别求出△AOD的三个内角即可得出结论.
(1)证明:∵△ABC为等边三角形
∴∠ACB=60°
∵△BOC绕点C按顺时针方向旋转60°得△ADC
∴∠OCB=∠DCA,OC=DC
∴∠OCB+∠ACO=∠DCA+∠ACO
∴∠ACB=∠OCD=60°
∴△COD是等边三角形
(2)解:∵△COD是等边三角形
∴∠CDO=60°
∵∠ADO=90°
∴∠ADC=∠CDO+∠ADO=60°+90°=150°
∵△BOC绕点C按顺时针方向旋转60°得△ADC
∴ α=∠ADC=150°
(3)解:当α=110°或125°或140°时,△AOD均是等腰三角形
当α=110°时,理由如下:
∴α=∠ADC=110°
∵∠ADO=∠ADC -∠CDO =50°,∠AOD=360°-∠AOB-α-∠COD =80°
∴∠OAD=180°-∠ADO -∠AOD =50°=∠ADO
∴△AOD是等腰三角形;
当α=125°时,理由如下:
∴α=∠ADC=125°
∵∠ADO=∠ADC -∠CDO =65°,∠AOD=360°-∠AOB-α-∠COD =65°
∴∠ADO =∠AOD
∴△AOD是等腰三角形;
当α=140°时,理由如下:
∴α=∠ADC=140°
∵∠ADO=∠ADC -∠CDO =80°,∠AOD=360°-∠AOB-α-∠COD =50°
∴∠OAD=180°-∠ADO -∠AOD =50°=∠AOD
∴△AOD是等腰三角形
以上证明方法任选其一即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于点E,交BA的延长线于点F.

(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)若PE=2,EF=6,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办园博会知识竞赛,打算购买A、B两种奖品.如果购买A奖品10件、B奖品5件,共需120元;如果购买A奖品5件、B奖品10件,共需90元.
(1)A,B两种奖品每件各多少元?
(2)若购买A、B奖品共100件,总费用不超过600元,则A奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
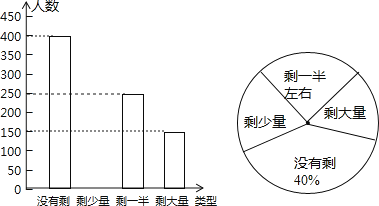
(1)这次被调查的同学共有 名;
(2)补全条形统计图;
(3)计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校20000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校![]() 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.

(1)![]() _____________,
_____________,![]() _______________;
_______________;
(2)请补全上图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;
(4)在抽查的![]() 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
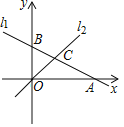
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
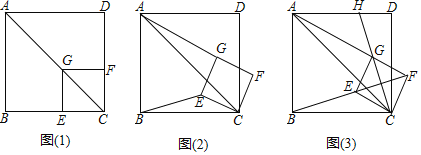
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,GF⊥CD.
(1)①求证:四边形CEGF是正方形;②推断:![]() 的值为 :
的值为 :
(2)将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系;
(3)正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,求正方形CEGF和正方形ABCD的边长.
,求正方形CEGF和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com