
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.

 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
(1)求证:AE=BG
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°)如图2所示,判断(1)中的结论是否仍然成立?如果仍成立,请给予证明;如果不成立,请说明理由;
(3)若BC=DE=4,当旋转角α为多少度时,AE取得最大值?直接写出AE取得最大值时α的度数,并利用备用图画出这时的正方形DEFG,最后求出这时AF的值.
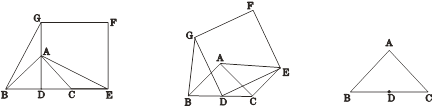
图1 图2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向西骑行10km到达A村,继续向西骑行30km到达B村,然后向东骑行70km到达C村,最后回到邮局。
(1)以邮局为原点,向东方向为正方向,用1cm表示10km,画出数轴,并在该数轴上表示A、B、C三个村庄的位置;
(2)A村离C村有多远?
(3)若摩托车每千米耗油0.1升,则该邮递员本次一共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为_____
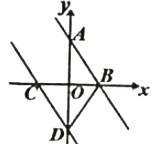
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…则第n个图形有__个小圆.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,AB两地之间有一座山,以前从A地到B地需要经过C地.现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km;参考数据:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com