
【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
(1)求证:AE=BG
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°)如图2所示,判断(1)中的结论是否仍然成立?如果仍成立,请给予证明;如果不成立,请说明理由;
(3)若BC=DE=4,当旋转角α为多少度时,AE取得最大值?直接写出AE取得最大值时α的度数,并利用备用图画出这时的正方形DEFG,最后求出这时AF的值.
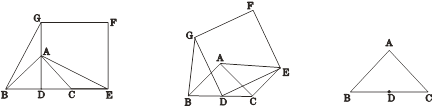
图1 图2 备用图
【答案】(1)证明见解析;(2)成立;(3)270°,![]()
【解析】试题分析(1)在Rt△BDG与Rt△EDA;根据边角边定理易得Rt△BDG≌Rt△EDA;故BG=AE;
(2)连接AD,根据直角三角形与正方形的性质可得Rt△BDG≌Rt△EDA;进而可得BG=AE;
(3)根据(2)的结论,求BG的最大值,分析可得此时F的位置,由勾股定理可得答案.
试题解析:(1)证明:∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD,
∴∠ADB=∠ADC=90°,AD=DC=DB,
∵四边形DEFG是正方形,
∴DE=DG,
∴△ADE≌△BDG(SAS),
∴BG=AE;
(2)成立;
理由如下:如图2,连接AD,
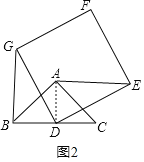
由(1)知AD=BD,AD⊥BC.
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°.
∴∠ADG+∠ADE=90°
∴∠BDG=∠ADE.
在△BDG和△ADE中,
∵BD=AD,∠BDG=∠ADE,GD=ED,
∴△BDG≌△ADE(SAS)
∴AE=BG;
(3)α=270°;
正方形DEFG如图3所示
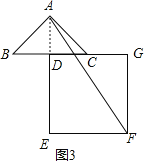
由(2)知BG=AE
∴当BG取得最大值时,AE取得最大值.
∵BC=DE=4,
∴EF=4,
∴BG=2+4=6
∴AE=6
在Rt△AEF中,由勾股定理,得
AF=![]() .
.


科目:初中数学 来源: 题型:
【题目】在数轴上有三个点![]() 、
、![]() 、
、![]() ,如图所示.
,如图所示.
![]()
(1)将点![]() 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________;
(2)将点![]() 向左平移3个单位得到数
向左平移3个单位得到数![]() ,再向右平移2个单位得到数
,再向右平移2个单位得到数![]() ,则
,则![]() ,
,![]() 分别是多少?
分别是多少?
(3)怎样移动![]() 、
、![]() 、
、![]() 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五·一”假期的某天,小明、小东两人同时分别从家出发骑共享单车到奥林匹克公园,已知小明家到公园的路程为15km,小东家到公园的路程为12km,小明骑车的平均速度比小东快3.5km/h,结果两人同时到达公园.求小东从家骑车到公园的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今,网上购物已成为一种新的消费时尚,精品书店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网
店(如图所示),已知两家网店的这种贺年卡的质量相同,请看图回答下列问题:
(1)假若精品书店想购买x张贺年卡,那么在甲、乙两家网店分别需要花多少钱(用含有x的式子表示)?(提示:如需付运费时运费只需付一次,即8元)
(2)精品书店打算购买300张贺年卡,选择哪家网店更省钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线.
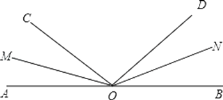
(1)当∠BOC=140°时,求∠AOM的度数;
(2)当∠AOC=30°,∠BOD=60°时,求∠MON的度数;
(3)当∠COD=x度时,则∠MON=________度.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
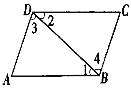
证明:∵ AB∥CD,
∴ ∠______=∠______ ( )
在△______和△______中,
∴ Δ______≌Δ______ ( ).
∴ ∠_____=∠____ ( )
∴ ______∥______ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如![]() ,我们来进行以下的探索:
,我们来进行以下的探索:
设![]() (其中a,b,m,n都是正整数),则有
(其中a,b,m,n都是正整数),则有![]() ,∴
,∴![]() ,
,![]() ,这样就得出了把类似
,这样就得出了把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都是正整数时,若![]() ,用含m,n的式子分别表示a,b,得a= ,b= ;
,用含m,n的式子分别表示a,b,得a= ,b= ;
(2)利用上述方法,找一组正整数a,b,m,n,填空:
﹣ ![]() =( —
=( — ![]() )2
)2
(3)![]() 且a,m,n都为正整数,求a的值.
且a,m,n都为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①13+(﹣22)﹣(﹣2)
②﹣4![]()
③(![]() ×(﹣48)
×(﹣48)
④﹣14﹣(![]() ﹣1)[﹣23+(﹣3)2]
﹣1)[﹣23+(﹣3)2]
(2)化简:①(3mn﹣2m2)+(﹣4m2﹣5mn)
②﹣(2a﹣3b)﹣2(﹣a+4b﹣1)
(3)先化简再求值:7x2y﹣2(2x2y﹣3xy2)-(4x2y﹣xy2),其中x=﹣2,y=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com