
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线.
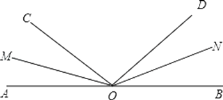
(1)当∠BOC=140°时,求∠AOM的度数;
(2)当∠AOC=30°,∠BOD=60°时,求∠MON的度数;
(3)当∠COD=x度时,则∠MON=________度.(请直接写出答案)
【答案】(1)20°;(2)135;(3)![]()
【解析】
(1)先求出∠AOC的度数,然后根据OM分别平分∠AOC即可求出∠AOM的度数;
(2)已知∠AOC、∠BOD度数且OM、ON分别平分∠AOC、∠BOD,可得∠AOM、∠BON度数,进而可得∠MON度数;
(3)由∠COD=α可知∠AOC+∠BOD=180°-α,根据角平分线可得∠AOC+∠BON=![]() (180°-α),进而可得∠MON.
(180°-α),进而可得∠MON.
(1) ∵∠AOB是平角,
∴∠AOC+∠COB=180°.
∵∠BOC=140°,
∴∠AOC=180°-140°=40°.
∵OM是∠AOC的平分线,
∴∠AOM=40°÷2=20°;
(2)∵∠AOB是平角,
∴∠AOB=180°.
∵OM、ON分别是∠AOC、∠BOD的平分线,
∴∠AOM=∠COM=∠AOC÷2, ∠BON=∠DON=∠BOD÷2,
∵∠AOC=30°,∠BOD=60°,
∴∠AOM=30°÷2=15°,∠BON=60°÷2=30°,
∴∠MON=180°-15°-30°=135°;
(3)∵OM、ON分别是∠AOC、∠BOD的角平分线,
∴∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=180°-∠AOM-∠BON
=180°-![]() ∠AOC-
∠AOC-![]() ∠BOD
∠BOD
=180°-![]() (∠AOC+∠BOD)
(∠AOC+∠BOD)
=180°-![]() (180°-∠COD)
(180°-∠COD)
=90°+![]() x
x
=![]() 度.
度.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
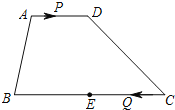
【题目】如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.
(1)当运动时间t为多少秒时,PQ∥CD.
(2)当运动时间t为多少秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
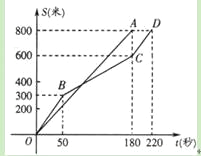
A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
| 1 | 3 |
| 4 | 5 | 6 | 7 | … |
y | … |
|
|
|
|
| 6 | 6 |
|
|
|
| m | … |
求m的值;
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
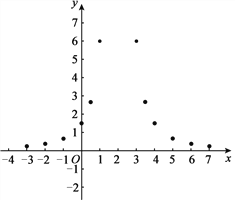
(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AC是对角线,点E,F,G分别为AB,AC,BC的中点:
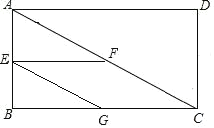
(1)求证:四边形EFCG是平行四边形;
(2)若ACD2ACB,AB4,求BF的长;
(3)在(2)的条件下,求四边形EFCG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
(1)求证:AE=BG
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°)如图2所示,判断(1)中的结论是否仍然成立?如果仍成立,请给予证明;如果不成立,请说明理由;
(3)若BC=DE=4,当旋转角α为多少度时,AE取得最大值?直接写出AE取得最大值时α的度数,并利用备用图画出这时的正方形DEFG,最后求出这时AF的值.
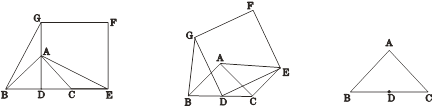
图1 图2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④
图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④ ![]() <0.其中正确结论的个数是( )
<0.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为_____
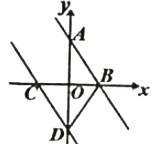
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com