
ЁОЬтФПЁПдФЖСРэНтЬтЃК
бЇЯАСЫЖўДЮИљЪНКѓЃЌФуЛсЗЂЯжвЛаЉКЌгаИљКХЕФЪНзгПЩвдаДГЩСэвЛИіЪНзгЕФЦНЗНЃЌШч![]() ЃЌЮвУЧРДНјаавдЯТЕФЬНЫїЃК
ЃЌЮвУЧРДНјаавдЯТЕФЬНЫїЃК
Щш![]() ЃЈЦфжаaЃЌbЃЌmЃЌnЖМЪЧе§ећЪ§ЃЉЃЌдђга
ЃЈЦфжаaЃЌbЃЌmЃЌnЖМЪЧе§ећЪ§ЃЉЃЌдђга![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЌетбљОЭЕУГіСЫАбРрЫЦ
ЃЌетбљОЭЕУГіСЫАбРрЫЦ![]() ЕФЪНзгЛЏЮЊЦНЗНЪНЕФЗНЗЈЃЎ
ЕФЪНзгЛЏЮЊЦНЗНЪНЕФЗНЗЈЃЎ
ЧыЗТееЩЯЪіЗНЗЈЬНЫїВЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБaЃЌbЃЌmЃЌnЖМЪЧе§ећЪ§ЪБЃЌШє![]() ЃЌгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОaЃЌbЃЌЕУa= ЁЁЃЌb=ЁЁ ЁЁЃЛ
ЃЌгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОaЃЌbЃЌЕУa= ЁЁЃЌb=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉРћгУЩЯЪіЗНЗЈЃЌеввЛзще§ећЪ§aЃЌbЃЌmЃЌnЃЌЬюПеЃК
ЁЁ ЁЁЉЁЁ ЁЁ![]() =ЃЈЁЁ ЁЊ
=ЃЈЁЁ ЁЊ ![]() ЃЉ2
ЃЉ2
ЃЈ3ЃЉ![]() ЧвaЃЌmЃЌnЖМЮЊе§ећЪ§ЃЌЧѓaЕФжЕЃЎ
ЧвaЃЌmЃЌnЖМЮЊе§ећЪ§ЃЌЧѓaЕФжЕЃЎ
ЁОД№АИЁП(1)a=m+5n,b=2mn;(2)МћНтЮі;(3)9Лђ21.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЭъШЋЦНЗНЙЋЪНАбЃЈm-n![]() ЃЉ2еЙПЊМДПЩЕУЕНгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОГіaЃЌbЃЛ
ЃЉ2еЙПЊМДПЩЕУЕНгУКЌmЃЌnЕФЪНзгЗжБ№БэЪОГіaЃЌbЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕФБэДяЪНЃЌСюm=2ЃЌn=1ЃЌдђПЩМЦЫуГіЖдгІЕФaКЭbЕФжЕЃЛ
ЃЈ3ЃЉРћгУЃЈ1ЃЉЕФНсЙћЕУЕН2mn=4ЃЌдђmn=2ЃЌдйРћгУmЃЌnЖМЮЊе§ећЪ§ЕУЕНm=2ЃЌn=1Лђm=1ЃЌn=2ЃЌШЛКѓМЦЫуЖдгІЕФaЕФжЕМДПЩЃЎ
(1)Ёп![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉД№АИВЛЮЈвЛ; ШЁm=2ЃЌn=1ЃЌ
дђa=4+5=9ЃЌb=4ЃЛ
(3)Ёп2mn=4ЃЌ
Ёрmn=2ЃЌ
ЖјmЃЌnЖМЮЊе§ећЪ§ЃЌ
Ёрm=2ЃЌn=1Лђm=1ЃЌn=2ЃЌ
ЕБm=2ЃЌn=1ЪБЃЌa=9ЃЛ
ЕБm=1ЃЌn=2ЪБЃЌa=21.
МДaЕФжЕЮЊ9Лђ21.
ЙЪД№АИЮЊЃК(1)a=m+5n,b=2mn;(2)МћНтЮі;(3)9Лђ21.


 ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ
ПкЫуаФЫуЫйЫугІгУЬтЯЕСаД№АИ ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
ЭЌВНЭиеЙдФЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
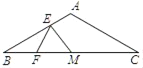
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃН4ЃЌЁЯBACЃН120ЁуЃЌMЪЧBCЕФжаЕуЃЌЕуEЪЧABБпЩЯЕФЖЏЕуЃЌЕуFЪЧЯпЖЮBMЩЯЕФЖЏЕуЃЌдђME+EFЕФзюаЁжЕЕШгк____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаетбљвЛИіЮЪЬтЃКЬНОПКЏЪ§![]() ЕФЭМЯѓгыаджЪЃЎ
ЕФЭМЯѓгыаджЪЃЎ
аЁЛЊИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОП.ЯТУцЪЧаЁЛЊЕФЬНОПЙ§ГЬ,ЧыВЙГфЭъећ:
ЕФЭМЯѓгыаджЪНјааСЫЬНОП.ЯТУцЪЧаЁЛЊЕФЬНОПЙ§ГЬ,ЧыВЙГфЭъећ:
(1)КЏЪ§![]() ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
(2)ЯТБэЪЧyгыxЕФМИзщЖдгІжЕ.
x | Ё | -3 | -2 | -1 | 0 |
| 1 | 3 |
| 4 | 5 | 6 | 7 | Ё |
y | Ё |
|
|
|
|
| 6 | 6 |
|
|
|
| m | Ё |
ЧѓmЕФжЕЃЛ
ЃЈ3ЃЉШчЯТЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕу.ИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
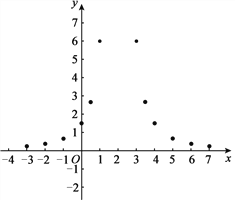
ЃЈ4ЃЉНсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФвЛЬѕаджЪЃК .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=90ЁуЃЌЕуDЪЧBCЕФжаЕуЃЎзїе§ЗНаЮDEFGЃЌЪЙЕуAЁЂCЗжБ№дкDGКЭDEЩЯЃЌСЌНгAEЃЌBGЃЎ
ЃЈ1ЃЉЧѓжЄЃКAE=BG
ЃЈ2ЃЉНЋе§ЗНаЮDEFGШЦЕуDФцЪБеыЗНЯђа§зЊІСЃЈ0ЁуЃМІСЁм360ЁуЃЉШчЭМ2ЫљЪОЃЌХаЖЯЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПШчЙћШдГЩСЂЃЌЧыИјгшжЄУїЃЛШчЙћВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєBC=DE=4ЃЌЕБа§зЊНЧІСЮЊЖрЩйЖШЪБЃЌAEШЁЕУзюДѓжЕЃПжБНгаДГіAEШЁЕУзюДѓжЕЪБІСЕФЖШЪ§ЃЌВЂРћгУБИгУЭМЛГіетЪБЕФе§ЗНаЮDEFGЃЌзюКѓЧѓГіетЪБAFЕФжЕЃЎ
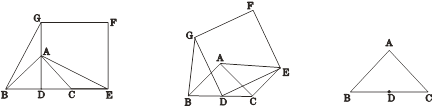
ЭМ1 ЭМ2 БИгУЭМ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкШЮвтгаРэЪ§aЃЌbЃЌЖЈвхдЫЫуЃКaЁбbЃНaЃЈa+bЃЉЉ1ЃЌЕШЪНгвБпЪЧЭЈГЃЕФМгЗЈЁЂМѕЗЈЁЂГЫЗЈдЫЫуЃЌР§ШчЃЌ2Ёб5ЃН2ЁСЃЈ2+5ЃЉЉ1ЃН13ЃЛЃЈЉ3ЃЉЁбЃЈЉ5ЃЉЃНЉ3ЁСЃЈЉ3Љ5ЃЉЉ1ЃН23ЃЎ
ЃЈ1ЃЉЧѓЃЈЉ2ЃЉЁб3![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЖдгкШЮвтгаРэЪ§mЃЌnЃЌЧыФужиаТЖЈвхвЛжждЫЫуЁАЈЁБЃЌЪЙЕУ5Ј3ЃН20ЃЌаДГіФуЖЈвхЕФдЫЫуЃКmЈnЃНЁЁ ЁЁЃЈгУКЌmЃЌnЕФЪНзгБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбЯТСаИїЪ§ЬюШыЯргІЕФМЏКЯФкЃК+8.5ЃЌ-3![]() ЃЌ0.3ЃЌ0ЃЌ-3.4ЃЌ12ЃЌ-9ЃЌ4
ЃЌ0.3ЃЌ0ЃЌ-3.4ЃЌ12ЃЌ-9ЃЌ4![]() ЃЌ-1.2ЃЌ-2.
ЃЌ-1.2ЃЌ-2.
ЃЈ1ЃЉе§Ъ§МЏКЯ:Ѓћ___________ЁЃ§ЃЛ
ЃЈ2ЃЉећЪ§МЏКЯ:Ѓћ___________ЁЃ§ЃЛ
ЃЈ3ЃЉЗЧе§ећЪ§МЏКЯ:Ѓћ_____________ЁЃ§ЃЛ
ЃЈ4ЃЉИКЗжЪ§МЏКЯ:Ѓћ ________________ЁЃ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§![]() ЭМЯѓЕФвЛВПЗжЃЌЭМЯѓЙ§ЕуA(-3ЃЌ0)ЃЌЖдГЦжсЮЊжБЯпx=Љ1ЃЌИјГіЫФИіНсТлЃКЂйcЃО0ЃЛЂкШєЕуB(-1.5ЃЌy1)ЁЂC(-2.5ЃЌy2)ЮЊКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђy1ЃМy2ЃЛЂл2aЉb=0ЃЛЂм
ЭМЯѓЕФвЛВПЗжЃЌЭМЯѓЙ§ЕуA(-3ЃЌ0)ЃЌЖдГЦжсЮЊжБЯпx=Љ1ЃЌИјГіЫФИіНсТлЃКЂйcЃО0ЃЛЂкШєЕуB(-1.5ЃЌy1)ЁЂC(-2.5ЃЌy2)ЮЊКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђy1ЃМy2ЃЛЂл2aЉb=0ЃЛЂм ![]() ЃМ0.Цфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
ЃМ0.Цфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ

A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=2x+2гыyжсНЛгкAЕуЃЌгыЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуMЃЌЙ§MзїMHЁЭxжсгкЕуHЃЌЧвtanЁЯAHO=2ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуMЃЌЙ§MзїMHЁЭxжсгкЕуHЃЌЧвtanЁЯAHO=2ЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉЕуNЃЈaЃЌ1ЃЉЪЧЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЭМЯѓЩЯЕФЕуЃЌдкxжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУPM+PNзюаЁЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈxЃО0ЃЉЭМЯѓЩЯЕФЕуЃЌдкxжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУPM+PNзюаЁЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛаЉАыОЖЯрЭЌЕФаЁдВАДШчЭМЫљЪОЕФЙцТЩАкЗХЃКЕк1ИіЭМаЮга6ИіаЁдВЃЌЕк2ИіЭМаЮга10ИіаЁдВЃЌЕк3ИіЭМаЮга16ИіаЁдВЃЌЕк4ИіЭМаЮга24ИіаЁдВЃЌЁдђЕкnИіЭМаЮга__ИіаЁдВЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com