
【题目】(本小题满分10分)
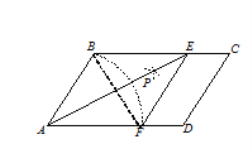
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

【答案】(1)详见解析;(2)60°.
【解析】
试题分析:(1)由作图过程可知,AB=AF,AE平分∠BAD,即可得∠BAE=∠EAF.再由四边形ABCD为平行四边形,可得BC∥AD,根据平行线的性质可得∠AEB=∠EAF,所以∠BAE=∠AEB,根据等腰三角形的性质可得AB=BE,即可得BE=AF,所以四边形ABEF为平行四边形,根据一组邻边相等的平行四边形是菱形即可判定四边形ABEF为菱形;(2)连接BF,已知四边形ABEF为菱形,根据菱形的性质可得BF与AE互相垂直平分,∠BAE=∠FAE,OA=![]() AE=
AE=![]() .再由菱形ABEF的周长为16,可得AF=4.所以cos∠OAF=
.再由菱形ABEF的周长为16,可得AF=4.所以cos∠OAF=![]() =
=![]() .即可得∠OAF=30°,所以∠BAF=60°.再由平行线的性质即可得∠C=∠BAD=60°.
.即可得∠OAF=30°,所以∠BAF=60°.再由平行线的性质即可得∠C=∠BAD=60°.
试题解析:
(1)由作图过程可知,AB=AF,AE平分∠BAD.∴∠BAE=∠EAF.
∵四边形ABCD为平行四边形,∴BC∥AD.∴∠AEB=∠EAF.
∴∠BAE=∠AEB,∴AB=BE.∴BE=AF.∴四边形ABEF为平行四边形.
∴四边形ABEF为菱形.
(2)连接BF,
![]()
∵四边形ABEF为菱形,∴BF与AE互相垂直平分,∠BAE=∠FAE.
∴OA=![]() AE=
AE=![]() .∵菱形ABEF的周长为16,∴AF=4.
.∵菱形ABEF的周长为16,∴AF=4.
∴cos∠OAF=![]() =
=![]() .∴∠OAF=30°,∴∠BAF=60°.
.∴∠OAF=30°,∴∠BAF=60°.
∵四边形ABCD为平行四边形,∴∠C=∠BAD=60°.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y= ![]() x﹣2
x﹣2 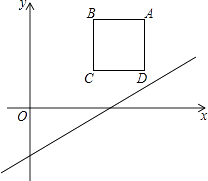
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
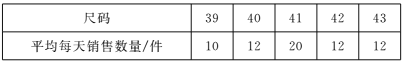
该店主决定本周进货时,增加一些41码的衬衫,影响该店主决策的统计量是( )
A.平均数 B.方差 C.众数 D.中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,与过
,与过![]() 点的直线相交于另一点
点的直线相交于另一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.
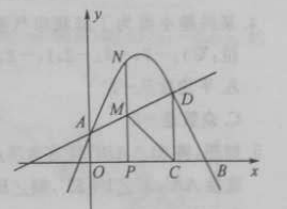
(1)求抛物线的表达式;
(2)点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() ,求
,求![]() 面积的最大值;
面积的最大值;
(3)若![]() 是
是![]() 轴正半轴上的一动点,设
轴正半轴上的一动点,设![]() 的长为,是否存在,使以点
的长为,是否存在,使以点![]() 为顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
为顶点的四边形是平行四边形?若存在,求出的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com