
【题目】如图,E为边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任一点,PQ⊥BC于Q,PR⊥BE于R.有下列结论:①△PCQ∽△PER;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论的个数是( )
.其中正确的结论的个数是( )
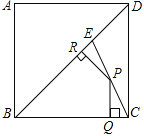
A.1B.2C.3D.4
【答案】D
【解析】
①根据两角对应相等的两个三角形相似,即可证出;②作△DCE的边DC上的高EF,根据三角形的面积公式即可得出△DCE的面积;③解直角△CEF,即可求出∠DCE的正切值;④连接BP,利用面积法求解,PQ+PR的值等于C点到BE的距离,即正方形对角线的一半.
解:①∵BE=BC,
∴∠QCP=∠REP,
又∵∠PQC=∠PRE=90°,
∴△PCQ∽△PER,故正确;
②作△DCE的边DC上的高EF.
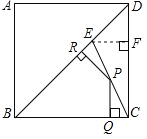
∵BE=BC=1,
∴DE=BD﹣BE=![]() ﹣1,
﹣1,
∵△DEF是等腰直角三角形,
∴EF=DF=![]() DE=
DE=![]() ,
,
∴S△DCE=![]() CDEF=
CDEF=![]() ,故正确;
,故正确;
③在△CEF中,∠EFC=90°,EF=![]() ,
,
CF=CD﹣DF=1﹣![]() =
=![]() ,
,
∴tan∠DCE=![]() =
=![]() ﹣1,故正确;
﹣1,故正确;
④连接BP,过C作CM⊥BD于M,
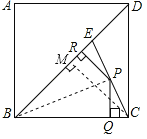
∵BC=BE,
∴S△BCE=S△BPE+S△BPC=BC×PQ×![]() +BE×PR×
+BE×PR×![]() =BC×(PQ+PR)×
=BC×(PQ+PR)×![]() =BE×CM×
=BE×CM×![]() ,∴PQ+PR=CM,
,∴PQ+PR=CM,
∵BE=BC=1且正方形对角线BD=![]() ,又BC=CD,CM⊥BD,
,又BC=CD,CM⊥BD,
∴为BD中点,又△BDC为直角三角形,
∴CM=![]() BD=
BD=![]() ,
,
∴PQ+PR=![]() ,故正确.
,故正确.
故选D.


科目:初中数学 来源: 题型:
【题目】某校举办园博会知识竞赛,打算购买A、B两种奖品.如果购买A奖品10件、B奖品5件,共需120元;如果购买A奖品5件、B奖品10件,共需90元.
(1)A,B两种奖品每件各多少元?
(2)若购买A、B奖品共100件,总费用不超过600元,则A奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
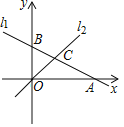
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
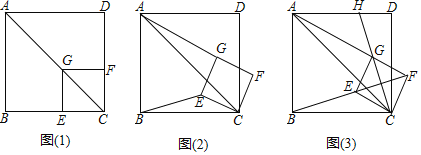
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,GF⊥CD.
(1)①求证:四边形CEGF是正方形;②推断:![]() 的值为 :
的值为 :
(2)将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系;
(3)正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,求正方形CEGF和正方形ABCD的边长.
,求正方形CEGF和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
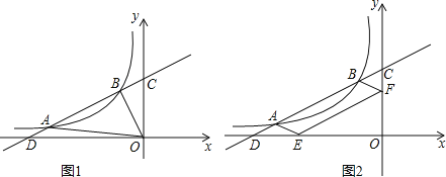
【题目】 如图,一次函数y=0.5x+3的图象与反比例函数y=![]() (k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(1)求此反比例函数的表达式和B点坐标;
(2)连接AO和BO,若点P在x轴上,且S△BDP=![]() S△BOA,求点P的坐标;
S△BOA,求点P的坐标;
(3)如图2,作ABFE,点F和点E分别在y轴和x轴上,求证:∠AED=∠FEO.
查看答案和解析>>
科目:初中数学 来源: 题型:
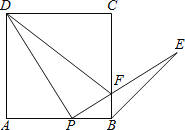
【题目】如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当△PFD∽△BFP时,求tan∠FPB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
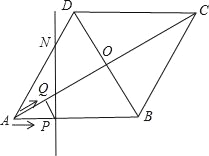
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2![]() cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com