
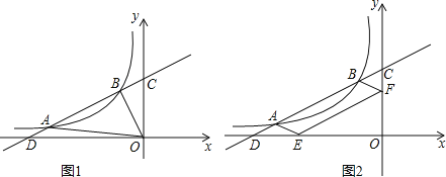
【题目】 如图,一次函数y=0.5x+3的图象与反比例函数y=![]() (k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(1)求此反比例函数的表达式和B点坐标;
(2)连接AO和BO,若点P在x轴上,且S△BDP=![]() S△BOA,求点P的坐标;
S△BOA,求点P的坐标;
(3)如图2,作ABFE,点F和点E分别在y轴和x轴上,求证:∠AED=∠FEO.
【答案】(1)y=-![]() ,点B的坐标为(-1,2.5);(2)点P的坐标为(-13.2,0)或(1.2,0);(3)详见解析
,点B的坐标为(-1,2.5);(2)点P的坐标为(-13.2,0)或(1.2,0);(3)详见解析
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A的坐标,由点A的坐标,利用反比例函数图象上点的坐标特征可求出k值,进而可得出反比例函数的表达式,再联立一次函数及反比例函数的表达式成方程组,通过解方程组即可求出点B的坐标;
(2)利用一次函数图象上点的坐标特征可求出点D的坐标,利用三角形的面积公式结合S△BDP=![]() S△BOA,即可求出DP的长度,再结合点D的坐标即可求出点P的坐标;
S△BOA,即可求出DP的长度,再结合点D的坐标即可求出点P的坐标;
(3)设点E的坐标为(m,0),点F的坐标为(0,n),利用平行四边形的对角线互相平分结合中点坐标公式,可得出关于m,n的二元一次方程组,解之即可求出点E的坐标,利用两点间的距离公式可求出AD=AE,进而可得出∠ADE=∠AED,由四边形ABFE为平行四边形可得出AB∥EF,利用平行线的性质可得出∠ADE=∠FEO,再结合∠ADE=∠AED即可证出∠AED=∠FEO.
解:(1)∵一次函数y=0.5x+3的图象过点A(-5,a),
∴a=0.5×(-5)+3=0.5,
∴点A的坐标为(-5,0.5).
∵反比例函数y=![]() (k≠0)的图象过点A(-5,0.5),
(k≠0)的图象过点A(-5,0.5),
∴k=-5×0.5=-2.5,
∴反比例函数的表达式为y=-![]() .
.
联立一次函数及反比例函数的表达式成方程组,得: ,
,
解得: ,
,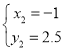 ,
,
∴点B的坐标为(-1,2.5).
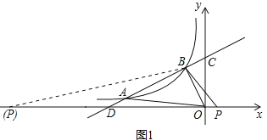
(2)当y=0时,0.5x+3=0,
解得:x=-6,
∴点D的坐标为(-6,0).
∵S△BDP=![]() S△BOA,
S△BOA,
∴![]() DP2.5=
DP2.5=![]() ×(
×(![]() ×6×2.5-
×6×2.5-![]() ×6×0.5),
×6×0.5),
∴DP=7.2,
∴点P的坐标为(-13.2,0)或(1.2,0).

(3)证明:设点E的坐标为(m,0),点F的坐标为(0,n).
∵四边形ABFE为平行四边形,且点A的坐标为(-5,0.5),点B的坐标为(-1,2.5),
∴![]() ,解得:
,解得:![]() ,
,
∴点E的坐标为(-4,0),点F的坐标为(0,2).
∵点D的坐标为(-6,0),点A的坐标为(-5,0.5),
∴AD=![]() =
=![]() ,AE=
,AE=![]() =
=![]() ,
,
∴AD=AE,
∴∠ADE=∠AED.
∵四边形ABFE为平行四边形,
∴AB∥EF,
∴∠ADE=∠FEO,
∴∠AED=∠FEO.


科目:初中数学 来源: 题型:
【题目】如图 ,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图象经过
的图象经过![]() .
.

(1)求抛物线的解析式;
(2)设抛物线与![]() 轴的另一个交的为
轴的另一个交的为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商品销售某种商品,平均每天可售出20件,每件盈利50元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若每件商品降价2元,则平均每天可售出______件;
(2)当每件商品降价多少元时,该商品每天的销售利润为1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
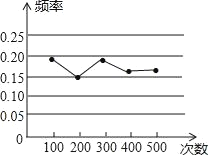
A. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
B. 掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C. 在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D. 袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任一点,PQ⊥BC于Q,PR⊥BE于R.有下列结论:①△PCQ∽△PER;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论的个数是( )
.其中正确的结论的个数是( )
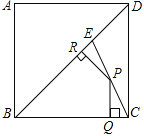
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为(1,4)的抛物线![]() 与直线
与直线![]() 交于点A(2,2),直线
交于点A(2,2),直线![]() 与
与![]() 轴交于点B与
轴交于点B与![]() 轴交于点C
轴交于点C
(1)求![]() 的值及抛物线的解析式
的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在![]() 轴上,求点P的坐标
轴上,求点P的坐标
(3)点D为![]() 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
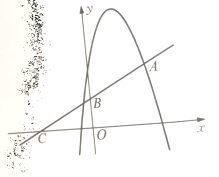
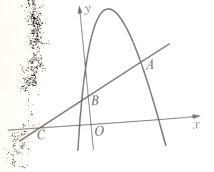
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待数字化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化阅读问卷调查表,请在表格中选择一项您最认同的观点,在其后空格内打“√”,非常感谢您的合作.
代码 | 观点 | |
| 获取信息方便,可以随时随地观看 | |
| 价格便宜易得 | |
| 使得人们成为“低头族”,不利于人际交往 | |
| 内容丰富,比纸质书涉猎更广 | |
| 其他 | |
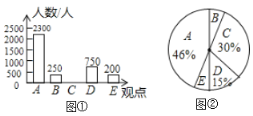
请根据统计图中提供的信息,解答下列问题:
(I)本次接受调查的总人数是__________人,并将条形统计图补充完整.
(Ⅱ)在扇形统计图中,观点![]() 的百分比是___________,表示观点
的百分比是___________,表示观点![]() 的扇形的圆心角度数为_________度.
的扇形的圆心角度数为_________度.
(Ⅲ)某市共有![]() 万人,请根据以上调查结果估算该市持
万人,请根据以上调查结果估算该市持![]() ,
,![]() ,
,![]() 观点赞成数字化阅读的人数共有多少万人.
观点赞成数字化阅读的人数共有多少万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com