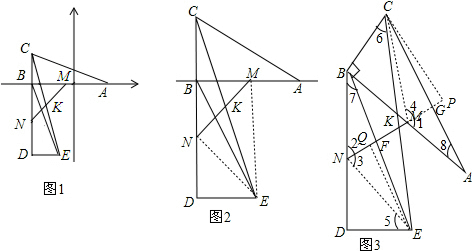
解(1)如图1,在Rt△BDE和Rt△ABC中,
∵
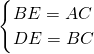
,
∴Rt△BDE≌Rt△ABC,
∴BD=AB,
∵C(-4,2),∠ABC=90°,
∴B(-4,0).
∵A(3,0),
∴AB=7,
∴BD=7
D(-4,-7);
(2)如图2,CK=EK
理由:连EM、CN,
∵AB=2BC,AB=BD,
∴BD=2BC,
∵M、N分别是AB、BD的中点,
∴AB=2BM,BD=2BN=2ND,
∴BC=BM=BN=DN,
∵DE=BC,
∴DE=DN.
∵∠ABC=∠BDE=90°,
∴∠DEN=∠DNE=∠BNM=∠BMN=45°,
∴∠MNE=180°-45°-45°=90°,
在△MBN和△NDE中,
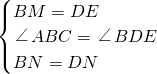
,
∴△MBN≌△NDE(SAS),
∴MN=EN,
∴△MNE是等腰直角三角形,
∴∠NME=45°,
∴∠BME=90°,
∴四边形BDEM是矩形,
∴EM=DB,BD∥EM,
∴EM=NC.∠CEM=∠NCE,∠NME=∠MNC,
在△EMK和△CNK中,

,
∴△EMK≌△CNK,
∴CK=EK.
(3)如图3,MN交BE、AC于F、G,过E、C作MN的垂线,垂足为Q、P,连结CM、EN,
∴∠EQN=∠EQK=∠CPM=90°.
∵AB=BD,M、N是AB、BD的中点,
∴DN=BN=BM=AM,
∴∠2=∠BMN,
∵∠1=∠BMN,
∴∠2=∠1.
在△EDN和△CBM中
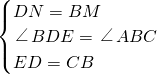
,
∴△EDN≌△CBM(SAS),
∴EN=CM.
在△BNE和△AMC中
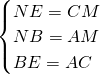
,
∴△BNE≌△AMC(SSS),
∴∠7=∠8,∠ENB=∠CMA,
∴∠ENB-∠2=∠CMA-∠1,
即∠3=∠4.
在△EQN和△CPM中,
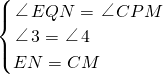
,
∴△EQN≌△CPM(AAS),
∴EQ=CP.
在△EQK和△CPK中,
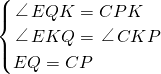
,
∴△EQK≌△CPK(AAS),
∴EK=CK.
,
分析:(1)证明△BDE≌△ABC,可得BD=AB,根据点M是AB的中点可求出BM的长度,继而可得点D的坐标;
(2)连接CM、BN,由已知易证得△ABC≌△BDE,可得到AB=BD;再通过证明△BCM≌△DEN,得CN=NE;接下来易证得△CMK≌△ENK,即可得CK=EK.
(3)过C、E分别作直线MK的垂线段,垂足分别为P、Q,首先证明△CMP≌△ENQ,可得PC=QE,然后易证明△CPQ≌△EQK,即得CK=EK.
点评:本题是一道综合型很强的试题,考查了全等三角形的判定及性质的运用,线段中点的运用,等腰直角三角形的性质的运用,点的坐标的运用,解答时灵活运用全等三角形的性质制造三角形全等是解答本题的关键.


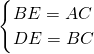 ,
,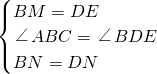 ,
, ,
,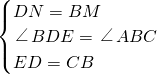 ,
,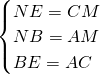 ,
,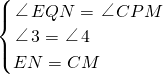 ,
,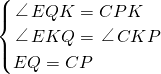 ,
, ,
,

 阅读快车系列答案
阅读快车系列答案 在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案.
在直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依此连接起来形成一个图案. 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,