
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).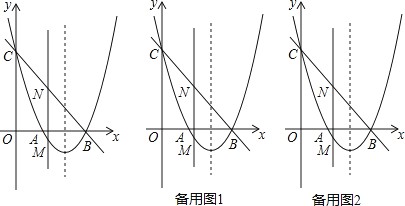
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:将点B(3,0)、C(0,3)代入抛物线y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣4x+3.
(2)
解:设点M的坐标为(m,m2﹣4m+3),设直线BC的解析式为y=kx+3,
把点点B(3,0)代入y=kx+3中,
得:0=3k+3,解得:k=﹣1,
∴直线BC的解析式为y=﹣x+3.
∵MN∥y轴,
∴点N的坐标为(m,﹣m+3).
∵抛物线的解析式为y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为x=2,
∴点(1,0)在抛物线的图象上,
∴1<m<3.
∵线段MN=﹣m+3﹣(m2﹣4m+3)=﹣m2+3m=﹣ ![]() +
+ ![]() ,
,
∴当m= ![]() 时,线段MN取最大值,最大值为
时,线段MN取最大值,最大值为 ![]() .
.
(3)
解:假设存在.设点P的坐标为(2,n).
当m= ![]() 时,点N的坐标为(
时,点N的坐标为( ![]() ,
, ![]() ),
),
∴PB= ![]() =
= ![]() ,PN=
,PN= ![]() ,BN=
,BN= ![]() =
= ![]() .
.
△PBN为等腰三角形分三种情况:
①当PB=PN时,即 ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
此时点P的坐标为(2, ![]() );
);
②当PB=BN时,即 ![]() =
= ![]() ,
,
解得:n=± ![]() ,
,
此时点P的坐标为(2,﹣ ![]() )或(2,
)或(2, ![]() );
);
③当PN=BN时,即 ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
此时点P的坐标为(2, ![]() )或(2,
)或(2, ![]() ).
).
综上可知:在抛物线的对称轴l上存在点P,使△PBN是等腰三角形,点的坐标为(2, ![]() )、(2,﹣
)、(2,﹣ ![]() )、(2,
)、(2, ![]() )、(2,
)、(2, ![]() )或(2,
)或(2, ![]() ).
).
【解析】(1)由点B、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)设出点M的坐标以及直线BC的解析式,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,结合点M的坐标即可得出点N的坐标,由此即可得出线段MN的长度关于m的函数关系式,再结合点M在x轴下方可找出m的取值范围,利用二次函数的性质即可解决最值问题;
(3)假设存在,设出点P的坐标为(2,n),结合(2)的结论可求出点N的坐标,结合点N、B的坐标利用两点间的距离公式求出线段PN、PB、BN的长度,根据等腰三角形的性质分类讨论即可求出n值,从而得出点P的坐标.
【考点精析】掌握二次函数的性质和两点间的距离是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 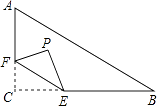
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(11,m)在第6段抛物线C6上,则m= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C(![]() 4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=
4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数y=![]() (k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为( )
(k≠0)图象上,当△ADE和△DCO的面积相等时,k的值为( )
A.-![]()
B.-![]()
C.-3![]()
D.-6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A为函数y= ![]() (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y= ![]() (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2的单位,这种点的运动称为点A的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5),已知点A的坐标为(1,0).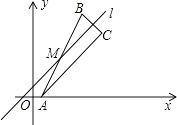
(1)分别写出点A经1次,2次斜平移后得到的点的坐标.
(2)如图,点M是直线l上的一点,点A关于点M的对称点的点B,点B关于直线l的对称轴为点C.
①若A、B、C三点不在同一条直线上,判断△ABC是否是直角三角形?请说明理由.
②若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),求出点B的坐标及n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xoy中,直线的参数方程为 ![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程,并指出其表示何种曲线;
(2)设直线l与曲线C交于A,B两点,若点P的直角坐标为(1,0),试求当 ![]() 时,|PA|+|PB|的值.
时,|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com