
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 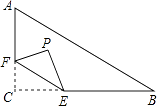
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米. 
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6.将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.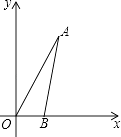
(1)请在图中画出△COD;
(2)求点A旋转过程中所经过的路程(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂分发年终奖金,具体金额和人数如下表所示,则下列对这组数据的说法中不正确的是( )
人 数 | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
金额(元) | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
A.极差是195000
B.中位数是15000
C.众数是15000
D.平均数是15000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,O是BC上一点,以点O为圆心,OB长为半径作圆,恰好经过点A,并与BC交于点D. 
(1)判断直线CA与⊙O的位置关系,并说明理由;
(2)若AB= ![]() ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,乘积的最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是 ;
(3)从中取出4张卡片.用学过的计算方法.使计算结果为24,请写出这个运算式.(至少写出两个)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[ ![]() ,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )
,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( ) 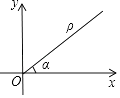
A.(﹣2,﹣2 ![]() )
)
B.(2,﹣2 ![]() )
)
C.(﹣2 ![]() ,﹣2)
,﹣2)
D.(﹣4,﹣4 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).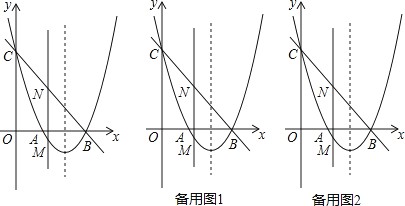
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com