
【题目】如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3)点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.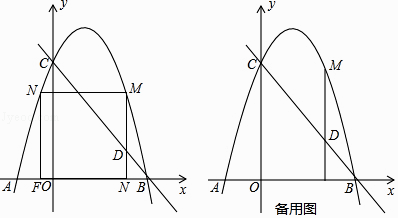
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;
(3)若∠DMN=90°,MD=MN,求点M的横坐标.
【答案】
(1)
解:∵抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),
∴设抛物线的函数解析式为y=a(x+1)(x﹣3),
将点C(0,3)代入上式,得:3=a(0+1)(0﹣3),
解得:a=﹣1,
∴所求抛物线解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3
(2)
解:由(1)知,抛物线的对称轴为x=﹣ ![]() =1,
=1,
如图1,设点M坐标为(m,﹣m2+2m+3),
∴ME=|﹣m2+2m+3|,
∵M、N关于x=1对称,且点M在对称轴右侧,
∴点N的横坐标为2﹣m,
∴MN=2m﹣2,
∵四边形MNFE为正方形,
∴ME=MN,
∴|﹣m2+2m+3|=2m﹣2,
分两种情况:
①当﹣m2+2m+3=2m﹣2时,解得:m1= ![]() 、m2=﹣
、m2=﹣ ![]() (不符合题意,舍去),
(不符合题意,舍去),
当m= ![]() 时,正方形的面积为(2
时,正方形的面积为(2 ![]() ﹣2)2=24﹣8
﹣2)2=24﹣8 ![]() ;
;
②当﹣m2+2m+3=2﹣2m时,解得:m3=2+ ![]() ,m4=2﹣
,m4=2﹣ ![]() (不符合题意,舍去),
(不符合题意,舍去),
当m=2+ ![]() 时,正方形的面积为[2(2+
时,正方形的面积为[2(2+ ![]() )﹣2]2=24+8
)﹣2]2=24+8 ![]() ;
;
综上所述,正方形的面积为24+8 ![]() 或24﹣8
或24﹣8 ![]()
(3)
解:设BC所在直线解析式为y=kx+b,
把点B(3,0)、C(0,3)代入表达式,得:
![]() ,解得:
,解得: ![]() ,
,
∴直线BC的函数表达式为y=﹣x+3,
设点M的坐标为(a,﹣a2+2a+3),则点N(2﹣a,﹣a2+2a+3),点D(a,﹣a+3),
①点M在对称轴右侧,即a>1,
则|﹣a+3﹣(﹣a2+2a+3)|=a﹣(2﹣a),即|a2﹣3a|=2a﹣2,
若a2﹣3a≥0,即a≤0或a≥3,a2﹣3a=2a﹣2,
解得:a= ![]() 或a=
或a= ![]() <1(舍去);
<1(舍去);
若a2﹣3a<0,即0≤a≤3,a2﹣3a=2﹣2a,
解得:a=﹣1(舍去)或a=2;
②点M在对称轴右侧,即a<1,
则|﹣a+3﹣(﹣a2+2a+3)|=2﹣a﹣a,即|a2﹣3a|=2﹣2a,
若a2﹣3a≥0,即a≤0或a≥3,a2﹣3a=2﹣2a,
解得:a=﹣1或a=2(舍);
若a2﹣3a<0,即0≤a≤3,a2﹣3a=2a﹣2,
解得:a= ![]() (舍去)或a=
(舍去)或a= ![]() ;
;
综上,点M的横坐标为 ![]() 、2、﹣1、
、2、﹣1、 ![]()
【解析】(1)待定系数法求解可得;(2)设点M坐标为(m,﹣m2+2m+3),分别表示出ME=|﹣m2+2m+3|、MN=2m﹣2,由四边形MNFE为正方形知ME=MN,据此列出方程,分类讨论求解可得;(3)先求出直线BC解析式,设点M的坐标为(a,﹣a2+2a+3),则点N(2﹣a,﹣a2+2a+3)、点D(a,﹣a+3),由MD=MN列出方程,根据点M的位置分类讨论求解可得.
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3 ![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE= ![]() CE;④S阴影=
CE;④S阴影= ![]() .其中正确结论的序号是 .
.其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小军做摸球游戏:A袋装有编号为1,2,3的三个小球,B袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数,则小华胜,否则小军胜,这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,FQ,当点Q停止运动时,△EFQ也停止运动.设运动时间为t(s)(0<t<6),解答下列问题:
(1)当t为何值时,PQ∥BD?
(2)设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于cm2 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com