
【题目】在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形. 
【答案】证明:∵AB∥DM, ∴∠BAM=∠AMD,
∵△ADC是由△ABC翻折得到,
∴∠CAB=∠CAD,AB=AD,BM=DM,
∴∠DAM=∠AMD,
∴DA=DM=AB=BM,
∴四边形ABMD是菱形.
【解析】只要证明AB=BM=MD=DA,即可解决问题.
【考点精析】本题主要考查了菱形的判定方法和翻折变换(折叠问题)的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )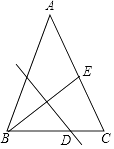
A.x﹣y2=3
B.2x﹣y2=9
C.3x﹣y2=15
D.4x﹣y2=21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3)点M、N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.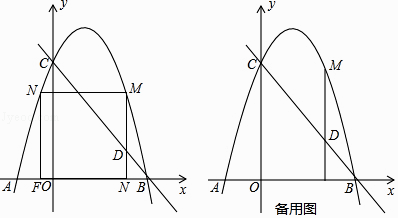
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;
(3)若∠DMN=90°,MD=MN,求点M的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y= ![]() x﹣
x﹣ ![]() 与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 .
与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 . 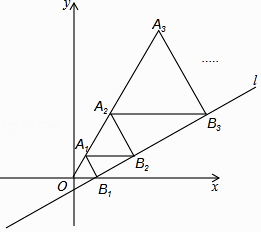
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F. 
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017宁夏)在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足. 
(1)求证:不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
(2)当BP的长为何值时,四边形AMPN的面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+b与双曲线y= ![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点. 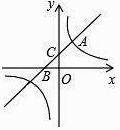
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某商场有一双向运行的自动扶梯,扶梯上行和下行的速度保持不变且相同,甲、乙两人同时站上了此扶梯的上行和下行端,甲站上上行扶梯的同时又以0.8m/s的速度往上跑,乙站上下行扶梯后则站立不动随扶梯下行,两人在途中相遇,甲到达扶梯顶端后立即乘坐下行扶梯,同时以0.8m/s的速度往下跑,而乙到达底端后则在原地等候甲.图2中线段OB、AB分别表示甲、乙两人在乘坐扶梯过程中,离扶梯底端的路程y(m)与所用时间x(s)之间的部分函数关系,结合图象解答下列问题: 
(1)求点B的坐标;
(2)求AB所在直线的函数表达式;
(3)乙到达扶梯底端后,还需等待多长时间,甲才到达扶梯底端?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB= ![]() ,∠C=120°,则点B′的坐标为( )
,∠C=120°,则点B′的坐标为( ) 
A.(3, ![]() )
)
B.(3, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com