
【题目】某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种与某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: 
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人多搬运了多少千克?
【答案】
(1)解:设yB关于x的函数解析式是yB=kx+b,
![]() ,得
,得 ![]() ,
,
答:yB关于x的函数解析式是yB=90x﹣90(1≤k≤6);
(2)解:由图象可得,
A种机器人屠呦呦的速度为:180÷3=60千克/小时,
B种机器人的速度为:180÷(3﹣1)=90千克/小时,
∴A、B两种机器人连续搬运5个小时,B种机器人多搬运了(90﹣60)×5=150(千克),
答:A、B两种机器人连续搬运5个小时,那么B种机器人多搬运了150千克.
【解析】(1)根据函数图象可以求得yB关于x的函数解析式;(2)根据函数图象可以去的两种机器人的速度,从而可以求得A、B两种机器人连续搬运5个小时,B种机器人多搬运了多少千克.


科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF. 
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在函数y=kx(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3(x3,y3),已知x1<x2<0<x3,则下列各式中正确的是( )
A. y1<0<y3 B. y3<0<y1 C. y2<y1<y3 D. y3<y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是全国最大的瓷碗造型建筑坐落于江西景德镇,整体造型概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为了计算该建筑物的横断面(瓷碗横断面ABCD为等腰梯形)的高度如图2,她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°,而后沿着一段坡度为0.44的小坡PQ步行到点Q(此过程中AD、AP、PQ始终处于同一平面)后测得点D的仰角减少了5°.
已知坡PQ的水平距离为20米,小敏身高忽略不计.
(1)试计算该瓷碗建筑物的高度?
(2)小敏测得AD与水平面夹角约为58°,底座直径AB约为20米,试计算碗口CD的直径为多少米?
坡度:坡与水平线夹角的正切值.
参考数据:sin40°≈0.64,tan40°≈0.84,sin58°≈0.85,tan58°≈1.60.


![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有35名同学参加眉山市的三苏文化知识竞赛,预赛分数各不相同,取前18名同学参加决赛. 其中一名同学知道自己的分数后,要判断自己能否进入决赛,只需要知道这35名同学分数的( ).
A. 众数 B. 中位数 C. 平均数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市120000名初中学生的视力情况,某校数学兴趣小组,并进行整理分析.
(1)小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.
(2)该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
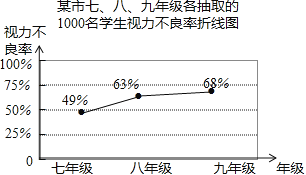
请你根据抽样调查的结果,估计该市120000名初中学生视力不良的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王班的同学去年6﹣12月区孔子学堂听中国传统文化讲座的人数如下表:
月份 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
人数 | 46 | 32 | 42 | 32 | 27 | 32 | 42 |
则该班去年6﹣12月去孔子学堂听中国传统文化讲座的人数的众数是( )
A.46
B.42
C.32
D.27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O半径为2,从⊙O外点C作⊙O的切线CA和CB,切点分别为点A和点D,∠ACB=90°,BC=2![]() ,则图中阴影部分的面积是________.
,则图中阴影部分的面积是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com