
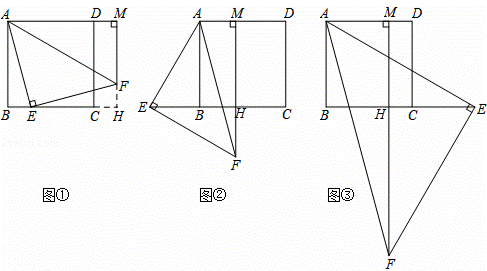
已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.
(1)当点E在边BC上,点M在边AD的延长线上时,如图①,求证:AB+BE=AM;
(提示:延长MF,交边BC的延长线于点H.)
(2)当点E在边CB的延长线上,点M在边AD上时,如图②;当点E在边BC的延长线上,点M在边AD上时,如图③.请分别写出线段AB,BE,AM之间的数量关系,不需要证明;
(3)在(1),(2)的条件下,若BE=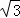 ,∠AFM=15°,则AM= 3﹣
,∠AFM=15°,则AM= 3﹣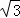 或
或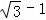 .
.
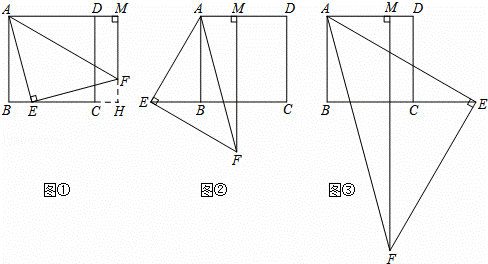
(1)证明:如图①,延长MF,交边BC的延长线于点H,
∵四边形ABCD是正方形,FM⊥AD,
∴∠ABE=90°,∠EHF=90°,四边形ABHM为矩形,
∴AM=BH=BE+EH
∵△AEF为等腰直角三角形,
∴AE=AF,∠AEB+∠FEH=90°,
∵∠EFH+∠FEH=90°,
∴∠AEB=∠EFH,
在△ABE与△EHF中,
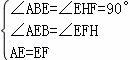 ,
,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∵AM=BH=BE+EH,
∴AM=BE+AB,即AB+BE=AM;
(2)解:如图②,∵∠AEB+∠FEH=90°,∠AEB+∠EAB=90°,
∴∠FEH=∠EAB,
在△ABE与△EHF中,
 ,
,
∴△ABE≌△EHF(AAS),
∴AB=EH=EB+AM;
如图③∠BAE+∠AEB=90°,∠AEB+∠HEF=90°,
∴∠BAE=∠HEF,
在△ABE与△EHF中,
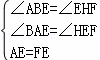 ,
,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∴BE=BH+EH=AM+AB;
(3)解:如图①,∵∠AFM=15°,∠AFE=45°,
∴∠EFM=60°,
∴∠EFH=120°,
在△EFH中,
∵∠FHE=90°,∠EFH=120°,
∴此情况不存在;
如图②,∵∠AFM=15°,∠AFE=45°,
∴∠EFH=60°,
∵△ABE≌△EHF,
∴∠EAB=∠EFH=60°,
∵BE=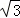 ,
,
∴AB=BE•tan60°=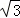 ×
×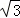 =3,
=3,
∵AB=EB+AM,
∴AM=AB﹣EB=3﹣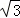 ;
;
如图③,∵∠AFM=15°,∠AFE=45°,
∴∠EFH=45°﹣15°=30°,
∴∠AEB=30°,
∵BE=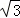 ,
,
∴AB=BE•tan30°=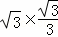 =1,
=1,
∵BE=AM+AB,
AM=BE﹣AB=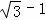 ,
,
故答案为:3﹣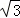 或
或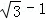 .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
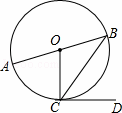
A. 40° B. 50° C. 80° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
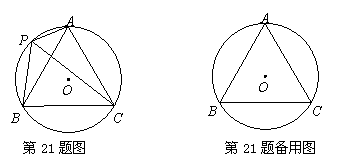
如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断 ABC的形状:______________;
ABC的形状:______________;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
 |
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.

(1)小华的问题解答:
(2)小明的问题解答:
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:选择题
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
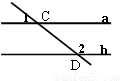
A.135° B.145° C.155° D.165°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,□ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于_________.
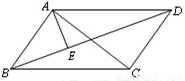
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com