
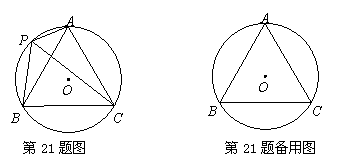
如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断 ABC的形状:______________;
ABC的形状:______________;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
 |
解:(1)等边三角形.
(2)PA+PB=PC.
证明:如图1,在PC上截取PD=PA,连接AD.
∵∠APC=60°,
∴△PAD是等边三角形.
 ∴PA=AD,∠PAD=60°.
∴PA=AD,∠PAD=60°.
又∵∠BAC=60°,
∴∠PAB=∠DAC.
∵AB=AC,
∴△PAB≌△DAC.
∴PB=DC.
∵PD+DC=PC,
∴PA+PB=PC.
 (3)当点P为
(3)当点P为 的中点时,四边形APBC面积最大.
的中点时,四边形APBC面积最大.
理由如下:如图2,过点P作PE⊥AB,垂足为E,
过点C作CF⊥AB,垂足为F,
∵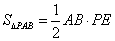 ,
,  .
.
∴S四边形APBC=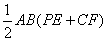 .
.
∵当点P为弧AB的中点时,PE+CF =PC, PC为⊙O直径,
∴四边形APBC面积最大.
又∵⊙O的半径为1,
 ∴其内接正三角形的边长AB=
∴其内接正三角形的边长AB= .
.
∴S四边形APBC= =
= .
.


科目:初中数学 来源: 题型:
下列运算正确的是( )
A. 5m+2m=7m2 B. ﹣2m2•m3=2m5
C. (﹣a2b)3=﹣a6b3 D. (b+2a)(2a﹣b)=b2﹣4a2
查看答案和解析>>
科目:初中数学 来源: 题型:
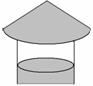 如图,要制作一个圆锥形
如图,要制作一个圆锥形 的烟囱帽,使底面圆的半径与母线长的比是4∶5.那么所需扇形铁皮的圆心角应为
的烟囱帽,使底面圆的半径与母线长的比是4∶5.那么所需扇形铁皮的圆心角应为
A.288° B.144°
C.216° D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50º,观测旗杆底部B的仰角为45º,则旗杆的高度约为________m.(结果精确到0.1m.参考数据:sin50º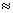 0.77,cos50º
0.77,cos50º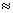 0.64,tan50º
0.64,tan50º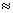 1.19)
1.19)

查看答案和解析>>
科目:初中数学 来源: 题型:
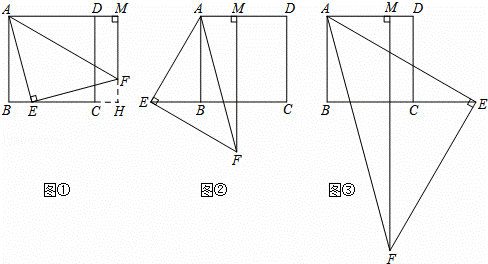
已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.
(1)当点E在边BC上,点M在边AD的延长线上时,如图①,求证:AB+BE=AM;
(提示:延长MF,交边BC的延长线于点H.)
(2)当点E在边CB的延长线上,点M在边AD上时,如图②;当点E在边BC的延长线上,点M在边AD上时,如图③.请分别写出线段AB,BE,AM之间的数量关系,不需要证明;
(3)在(1),(2)的条件下,若BE=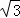 ,∠AFM=15°,则AM= 3﹣
,∠AFM=15°,则AM= 3﹣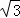 或
或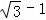 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都区七校联谊九年级3月月考数学试卷(解析版) 题型:填空题
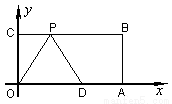
如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com