
【题目】如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,给出下列结论:①∠AME=108°;②![]() ;③MN=
;③MN=![]() ;④
;④![]() .其中正确结论的序号是________.
.其中正确结论的序号是________.
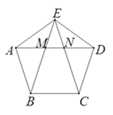
【答案】①、②、③
【解析】分析:根据正五边形的性质得到∠ABE=∠AEB=∠EAD=36°,根据三角形的内角和即可得到结论;由于∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,得到∠AEN=∠ANE,根据等腰三角形的判定定理得到AE=AN,同理DE=DM,根据相似三角形的性质得到和AM,AN,AD有关的比例式,等量代换得到AN2=AMAD;根据AE2=AMAD,列方程得到MN=3-![]() ;在正五边形ABCDE中,由于BE=CE=AD=1+
;在正五边形ABCDE中,由于BE=CE=AD=1+![]() ,得到BH=
,得到BH=![]() BC=1,根据勾股定理得到EH的值,根据三角形的面积得到结论.
BC=1,根据勾股定理得到EH的值,根据三角形的面积得到结论.
详解:∵∠BAE=∠AED=108°,
∵AB=AE=DE,
∴∠ABE=∠AEB=∠EAD=36°,
∴∠AME=180°-∠EAM-∠AEM=108°,故①正确;
∵∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,
∴∠AEN=∠ANE,
∴AE=AN,
同理DE=DM,
∴AE=DM,
∵∠EAD=∠AEM=∠ADE=36°,
∴△AEM∽△ADE
∴![]() ,
,
∴AE2=AMAD;
∴AN2=AMAD;故②正确;
∵AE2=AMAD,
∴22=(2-MN)(4-MN),
解得:MN=3-![]() ;故③正确;
;故③正确;
在正五边形ABCDE中,过E作EH⊥BC于H

∵BE=CE=AD=1+![]() ,
,
∴BH=![]() BC=1,
BC=1,
∴EH=![]() ,
,
∴S△EBC=![]() BCEH=
BCEH=![]() ×2×
×2×![]() =
=![]() ,故④错误;
,故④错误;
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】问题1:设a、b是方程x2+x-2012=0的两个实数根,则a2+2a+b的值为________;
问题2:方程x2-2x-1=0的两个实数根分别为x1,x2,则(x1―1)(x2―1)=_______;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一水箱,它的容积为500L,水箱内原有水200L,现往水箱中注水,已知每分钟注水10L.
(1)写出水箱内水量![]() (L)与注水时间
(L)与注水时间![]() (min)的函数关系.
(min)的函数关系.
(2)求注水12min时水箱内的水量?
(3)需多长时间把水箱注满?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
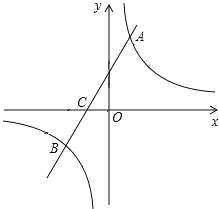
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
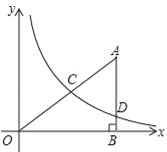
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠B=30°,点D在BC上,过点D作DE⊥BC,交BA或其延长线于点E,过点E作EF⊥BA交AC或其延长线于点F,连接DF.若DF⊥AC,则BD=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
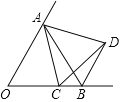
A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com