
【题目】在一次机器人测试中,要求机器人从A出发到达B处.如图1,已知点A在O的正西方600cm处,B在O的正北方300cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20cm/秒,在射线AO的左侧(AO上方)区域的速度为10cm/秒. 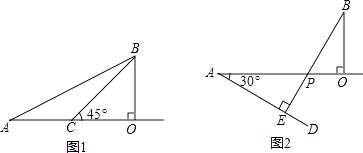
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236,
≈2.236, ![]() ≈2.449)
≈2.449)
(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);
(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);
(3)如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.
【答案】
(1)解:沿A→O→B路线行进所用时间为:600÷20+300÷10=60(秒),
在Rt△OBA中,由勾股定理,得AB= ![]() =300
=300 ![]() (cm).
(cm).
∴沿A→B路线行进所用时间为:300 ![]() ÷10≈300×2.236÷10≈67(秒)
÷10≈300×2.236÷10≈67(秒)
(2)解:在Rt△OBC中,OB=300,∠OCB=45°,∴OC=OB=300cm,BC= ![]() =300
=300 ![]() (cm),
(cm),
∴AC=600﹣300=300(cm).
∴沿A→C→B路线行进所用时间为:AC÷20+BC÷10=300÷20+300 ![]() ÷10≈15+42.42≈57(秒)
÷10≈15+42.42≈57(秒)
(3)解:在AO上任取异于点P的一点P′,作P′E′⊥AD于E′,连接P′B,
在Rt△APE和Rt△AP′E′中,sin30°= ![]() =
= ![]() ,∴EP=
,∴EP= ![]() ,E′P′=
,E′P′= ![]() .
.
∴沿A→P→B路线行进所用时间为:AP÷20+PB÷10=EP÷10+PB÷10=(EP+PB)÷10= ![]() BE(秒),
BE(秒),
沿A→P′→B路线行进所用时间为:
AP′÷20+P′B÷10=E′P′÷10+P′B÷10=(E′P′+P′B)÷10= ![]() (E′P′+P′B)(秒).
(E′P′+P′B)(秒).
连接BE′,则E′P′+P′B>BE′>BE,∴ ![]() BE<
BE< ![]() (E′P′+P′B).
(E′P′+P′B).
∴沿A→P→B路线行进所用时间,小于沿A→P′→B路线行进所用时间.
即机器人沿A→P→B路线行进所用时间最短
【解析】(1)根据已知先求出沿A→O→B路线行进所用时间,然后由勾股定理求出AB,从而求出沿A→B路线行进所用时间;(2)首先解Rt△OBC,运用三角函数求出BC,继而得出AC,从而求出沿A→C→B路线到达B处所用的时间;(3)在AO上任取异于点P的一点P′,作P′E′⊥AD于E′,连接P′B,分别求出沿A→P→B路线行进所用时间和沿A→P′→B路线行进所用时间进行比较得出结论.
【考点精析】根据题目的已知条件,利用等腰直角三角形和含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K. 
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE= ![]() ,AK=2
,AK=2 ![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y= ![]() (x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(x>0)的图象与一次函 数y=﹣x+b的图象分别交于A(1,3)、B两点.
(1)求m、b的值;
(2)若点M是反比例函数图象上的一动点,直线MC⊥x轴于C,交直线AB于点N,MD⊥y轴于D,NE⊥y轴于E,设四边形MDOC、NEOC的面积分别为S1、S2 , S=S2﹣S1 , 求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
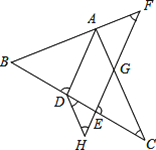
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照题中提供的思路点拨,先填空,然后完成解答的全过程.
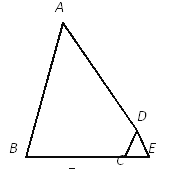
如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:(1)由已知条件AB=AD,∠BAD=60°,可知△ABD是_三角形.同理由已知条件∠BCD=120°得到∠DCE=_,且CE=CD,可知_;
(2)要证BC+DC=AC,可将问题转化为证两条线段相等,即_=_;
(3)要证(2)中所填写的两条线段相等,可以先证明_.请写出完整的证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com