
【题目】完成下面的证明.
已知:如图,![]() 与
与![]() 互补,
互补,![]() ,
,
求证:![]()

证明:![]() 与
与![]() 互补
互补
即![]() ,(已知)
,(已知)
![]() // ( )
// ( )
![]() .( )
.( )
又![]() ,(已知)
,(已知)
![]() ,即
,即![]() .(等式的性质)
.(等式的性质)
![]() // (内错角相等,两直线平行)
// (内错角相等,两直线平行)
![]() .( )
.( )
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
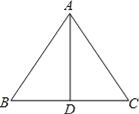
【题目】如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;②三角形的三条高所在的直线的交点可能在三角形的内部或外部;③多边形的所有内角中最多有3个锐角;④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.其中真命题的是_______________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB。
![]()
(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于P(x,y)作变换得到P′(﹣y+1,x+1),例如:A1(3,1)作上述变换得到A2(0,4),再将A2做上述变换得到A3___________,这样依次得到A1,A2,A3,…An;…,则A2018的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
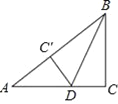
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数 ![]() 的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<﹣1时,一次函数值大于反比例函数值,当x>﹣1时,一次函数值小于反比例函数值.
的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<﹣1时,一次函数值大于反比例函数值,当x>﹣1时,一次函数值小于反比例函数值.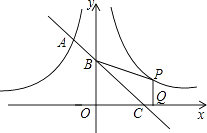
(1)求一次函数的解析式;
(2)设函数y2= ![]() 的图象与
的图象与 ![]() 的图象关于y轴对称,在y2=
的图象关于y轴对称,在y2= ![]() 的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com