练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．下列条件中，能判定四边形是平行四边形的条件是（　　）
    A．一组对边平行，另一组对边相等B．一组对边平行，一组对角相等
    C．一组对边平行，一组邻角互补D．一组对边相等，一组邻角相等

    分析 平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定，逐一验证．

    解答 解：A、一组对边相等，另一组对边平行，也有可能是等腰梯形；
    B、一组对边平行，一组对角相等，可得到两组对角分别相等，所以是平行四边形；
    C、一组对边平行，一组邻角互补，也有可能是等腰梯形；
    D、一组对边相等，一组邻角相等，不一定是平行四边形．
    故选：B．

    点评 本题考查平行四边形的判定，注意间接条件的应用．在应用判定定理判定平行四边形时，应仔细观察题目所给的条件，仔细选择适合于题目的判定方法进行解答，避免混用判定方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

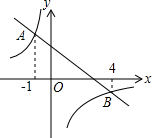    18．已知如图，一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点，使不等式ax+b＞$\frac{k}{x}$成立的自变量x的取值范围是（　　）
    A．x＜-1或x＞4B．-1＜x＜4C．x＜-1或0＜x＜4D．-1＜x＜0或x＞4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）${3^2}×（-\frac{1}{3}）+2$
    （2）${1^4}-\sqrt{16}÷{（-\frac{1}{2}）^2}+|{-3}|$
    （3）先化简再求值：-（3a2-2ab）+[3a2-（ab+2）]，其中$a=-\frac{1}{2}$，b=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．在函数y=（m+3）x+m-2中，当m≠-3时，是一次函数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．将满足条件“至少出现一个数字0，且是4的倍数的正整数”从小到大排成一列数：20，40，60，80，100，104，…，则这列数中的第159个数为2012．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．己知方程2xa+b-xa-b-ab=0是关于x的一元二次方程，则对应a、b的值有（　　）
    A．2组B．3组C．4组D．5组

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．设a，b为实数，已知关于x的方程x2-（a+b）x+$\frac{{a}^{2}+2{b}^{2}-2b+1}{2}$=0有两个实根．求a，b的取值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知xm=2，求（x3m）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

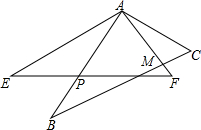    1．如图，在△ABC和△AEF中，∠B=∠E，AB=AE，BC=EF，∠BAE=24°，∠F=57°，边BC与AF相交于点M，边AB与EF相交于点P．
    （1）请说明∠BAE=∠CAF的理由；
    （2）△ABC可以经过图形的变换的得到△AEF，请你描述这个变换；
    （3）求∠AMB的度数．

    查看答案和解析>>

    同步练习册答案