
【题目】已知:等边△ABC的边长为2,点D为平面内一点,且BD=![]() AD=2
AD=2![]() ,则CD= .
,则CD= .
【答案】2或4
【解析】
试题分析:①根据等腰三角形的性质,可得DE的长,根据正弦函数,可得∠CAD的度数,根据等边三角形,可得CD的长;
②根据等腰三角形的性质,可得DE的长,根据正弦函数,可得∠EAD的度数,根据角的和差,可得A、C、D在同一条直线上,根据线段的和差,可得答案.
解:如图1:
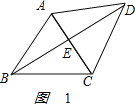
由BD=![]() AD=2
AD=2![]() ,得
,得
AD=AB=AC=2.
由等腰三角形的性质,得
DE=![]() .
.
sin∠DAE=![]() ,
,
∠DAE=60°,△ACD是等边三角形,
CD=AC=2;
如图2:
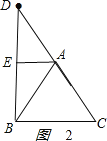 ,
,
由BD=![]() AD=2
AD=2![]() ,得
,得
AD=AB=AC=2.
由等边三角形的性质,得
DE=![]() ,∠DAE=∠BAE.
,∠DAE=∠BAE.
sin∠DAE=![]() ,
,
∠DAE=∠BAE=60°,
AD与AC在同一条直线上,
CD=AC=2;
CD=AD+AC=2+2=4.
故答案为:2或4.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.
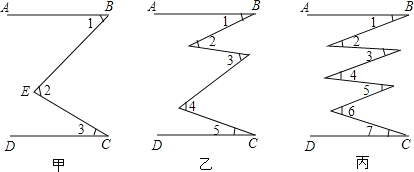
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次降价30%。那么顾客到__________家超市购买这种商品更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足:①![]() 与2x2+ay3的和是单项式; ②
与2x2+ay3的和是单项式; ②![]() ,
,
(1)求a、b、c的值;
(2)求代数式(5b2﹣3c2)﹣3(b2﹣c2)﹣(﹣c2)+2016abc的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com