
分析 首先根据立方根、算术平方根的定义可以列出关于a、b的方程组,解方程组即可求出a与b的值,再代入所求代数式,并结合立方根的定义即可得出结果.
解答 解:由题意,有$\left\{\begin{array}{l}{2a+b-3=2}\\{3a-2b+6=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$,
所以M=$\sqrt{1+3}=2$,N=$\root{3}{3-2}=1$,
把M=2,N=1代入2M+3N=4+3=7,
所以其立方根为:$\root{3}{7}$.
点评 本题考查了算术平方根和立方根的概念的运用,关键是根据立方根、算术平方根的定义可以列出关于a、b的方程组.


科目:初中数学 来源: 题型:填空题
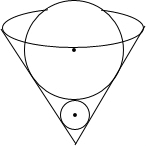 如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍.
如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com