
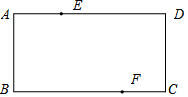
 如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形.
如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形. 分析 如图,连接AC、BD交于点O,过点O作BD的垂线交AD于E,交BC于F.则四边形DEBF是菱形,根据邻边相等四边形是菱形即可证明.
解答 解:如图,连接AC、BD交于点O,过点O作BD的垂线交AD于E,交BC于F.则四边形DEBF是菱形.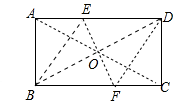
理由:∵四边形ABCD是矩形,
∴OB=OD,AD∥BC,
∴∠EDB=∠FBO.
在△EDO和△FBO中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{DO=OB}\\{∠EOD=∠FOB}\end{array}\right.$,
∴△EDO≌△FBO,
∴DE=BF,∵DE∥BF,
∴四边形DEBF是平行四边形,
∵OB=OD,EO⊥BD,
∴EB=ED,
∴四边形DEBF是菱形.
点评 本题考查矩形的性质、菱形的判定等知识,解题的关键是熟练掌握矩形的性质,菱形的判定,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
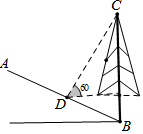 如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
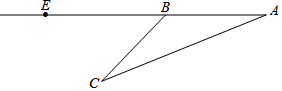 日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com