

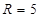 ;(2)
;(2)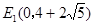 ,
,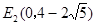 ,
,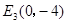 ,
,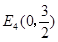
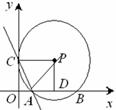
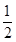 AB=3
AB=3 ,
,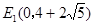 ,
,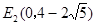 ,
,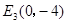 ,
,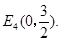


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点
,点 的坐标是
的坐标是 ,以点
,以点 为顶点的抛物线
为顶点的抛物线 经过
经过 轴上的点
轴上的点 .
.
 的坐标;
的坐标; ,求平移后抛物线的解析式.
,求平移后抛物线的解析式. 查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=-2x2-12x+16 | B.y=-2x2+12x-16 |
| C.y=-2x2+12x-19 | D.y=-2x2+12x-20 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
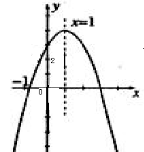
 的图象如图所示,则下列结论:
的图象如图所示,则下列结论:
 的两根之和大于1;②
的两根之和大于1;② ;
; 随
随 的增大而增大;④
的增大而增大;④ .
.| A.4个 | B.3个 | C.2个 | D.1个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 万元援助灾区
万元援助灾区 所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第
所学校,用于搭建帐篷和添置教学设备。根据各校不同的受灾情况,该企业捐款的分配方案如下:所有学校得到的捐款数都相等,到第 所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中
所学校的捐款恰好分完,捐款的分配方法如下表所示. (其中 ,
, ,
,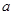 都是正整数)
都是正整数)
 与
与 的关系式;
的关系式; 时,该企业能援助多少所学校?
时,该企业能援助多少所学校? 万元的捐款,按照原来的分配方案援助其它学校.若
万元的捐款,按照原来的分配方案援助其它学校.若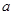 由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?
由 (2)确定,则再次提供的捐款最多又可以援助多少所学校?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com