
ЎҫМвДҝЎҝДі№Өі§ІНМьјЖ»®№әВт12ХЕІНЧАәНТ»ЕъІНТОЈ¬ПЦФЪҙУјЧЎўТТБҪЙМіЎБЛҪвөҪЈ¬Н¬Т»РНәЕөДІНЧАұЁјЫГҝХЕҫщОӘ200ФӘЈ¬ІНТОұЁјЫГҝ°СҫщОӘ50ФӘЈ¬јЧЙМіЎЧц»о¶ҜЈ¬Гҝ№әВтТ»ХЕІНЧАФщЛНТ»°СІНТОЎЈТТЙМіЎөД»о¶ҜКЗЛщУРЧАТОҫщ°ҙұЁјЫөД°ЛОеХЫПъКЫЎЈИфёГ№Өі§јЖ»®№әВтІНТО![]() (
(![]() Јҫ12)°СЈ¬ФтЈә
Јҫ12)°СЈ¬ФтЈә
ЈЁ1Ј©өұ№әВт40°СІНТОКұЈ¬өҪДДјТЙМіЎ№әВт»®ЛгЈҝ
ЈЁ2Ј©УГә¬![]() өДҙъКэКҪұнКҫөҪјЧЎўТТБҪЙМіЎ№әВтЛщРиТӘөД·СУГЎЈ
өДҙъКэКҪұнКҫөҪјЧЎўТТБҪЙМіЎ№әВтЛщРиТӘөД·СУГЎЈ
ЈЁ3Ј©өұ№әВт¶аЙЩ°СІНТОКұЈ¬өҪјЧЎўТТБҪЙМіЎ№әВтЛщРиТӘөД·СУГПаН¬Јҝ
Ўҫҙр°ёЎҝЈЁ1Ј©өұ№әВтЧАТО40°СКұЈ¬өҪТТЙМіЎИҘВт»®ЛгЈ»ЈЁ2Ј©![]() Ј¬
Ј¬![]() Ј»ЈЁ3Ј©өұ№әВт32°СІНТОКұЈ¬өҪјЧЎўТТБҪЙМіЎ№әВтЛщРиТӘөД·СУГПаН¬.
Ј»ЈЁ3Ј©өұ№әВт32°СІНТОКұЈ¬өҪјЧЎўТТБҪЙМіЎ№әВтЛщРиТӘөД·СУГПаН¬.
ЎҫҪвОцЎҝ
ЈЁ1Ј©·ЦұрјЖЛгјЧТТБҪёцЙМјТЛщРиТӘөД·СУГЈ¬ҪшРРұИҪПЈ¬јҙҝЙөГөҪҙр°ёЈ»
ЈЁ2Ј©ёщҫЭМвТвЈ¬ХТіцөИБҝ№ШПөЈ¬БРіц№ШПөКҪјҙҝЙЈ»
ЈЁ3Ј©УЙЈЁ2Ј©өДҪбВЫЈ¬БоБҪёцЙМјТөД·СУГПаөИЈ¬јҙҝЙЗуіцТОЧУөДКэБҝ.
ҪвЈәЈЁ1Ј©![]() КұЈ¬
КұЈ¬
![]() ФӘЈ¬
ФӘЈ¬
![]() ФӘЈ¬
ФӘЈ¬
ЎЯ3800Јҫ3740 Ј¬
ЎаТТәПККЈ»
Ўаөұ№әВтЧАТО40°СКұЈ¬өҪТТЙМіЎИҘВт»®ЛгЎЈ
ЈЁ2Ј©Йи№әВт12ХЕІНЧАәН![]() °СІНТОЈ¬өҪ№әВтјЧЙМіЎөД·СУГОӘ
°СІНТОЈ¬өҪ№әВтјЧЙМіЎөД·СУГОӘ![]() ФӘЈ¬өҪТТЙМіЎ№әВтөД·СУГОӘ
ФӘЈ¬өҪТТЙМіЎ№әВтөД·СУГОӘ![]() ФӘ. УЙМвТвөГЈә
ФӘ. УЙМвТвөГЈә
![]() Ј»
Ј»
![]() Ј»
Ј»
ЈЁ3Ј©өҪјЧЎўТТБҪЙМіЎ№әВтЛщРиТӘөД·СУГПаН¬Ј¬
Бо![]() Ј¬Фт
Ј¬Фт
![]() Ј¬
Ј¬
ҪвөГЈә![]()
Ўаөұ№әВт32°СІНТОКұЈ¬өҪјЧЎўТТБҪЙМіЎ№әВтЛщРиТӘөД·СУГПаН¬.


 МмМмБ·ҝЪЛгПөБРҙр°ё
МмМмБ·ҝЪЛгПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРЛө·ЁХэИ·өДКЗЈЁЎЎЎЎЈ©
A. Ў°ГчМмҪөУкөДёЕВККЗ60%ЎұұнКҫГчМмУР60%өДКұјд¶јФЪҪөУк
B. Ў°ЕЧТ»Г¶УІұТХэГжіҜЙПөДёЕВКОӘ![]() ЎұұнКҫГҝЕЧ2ҙОҫНУРТ»ҙОХэГжіҜЙП
ЎұұнКҫГҝЕЧ2ҙОҫНУРТ»ҙОХэГжіҜЙП
C. Ў°ІКЖұЦРҪұөДёЕВКОӘ1%ЎұұнКҫВт100ХЕІКЖұҝП¶Ё»бЦРҪұ
D. Ў°ЕЧТ»Г¶Хэ·ҪМеч»ЧУЈ¬іҜЙПөДөгКэОӘ2өДёЕВКОӘ![]() ЎұұнКҫЛжЧЕЕЧЦАҙОКэөДФцјУЈ¬Ў°ЕЧіціҜЙПөДөгКэОӘ2ЎұХвТ»КВјю·ўЙъөДёЕВКОИ¶ЁФЪ
ЎұұнКҫЛжЧЕЕЧЦАҙОКэөДФцјУЈ¬Ў°ЕЧіціҜЙПөДөгКэОӘ2ЎұХвТ»КВјю·ўЙъөДёЕВКОИ¶ЁФЪ![]() ёҪҪь
ёҪҪь
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј1Ј¬өгOОӘЦұПЯABЙПТ»өгЈ¬№эөгOЧчЙдПЯOCЈ¬К№ЎПBOCЈҪ120ЎгЈ®Ҫ«Т»ЦұҪЗИэҪЗРОөДЦұҪЗ¶Ҙөг·ЕФЪөгOҙҰЈ¬Т»ұЯOMФЪЙдПЯOBЙПЈ¬БнТ»ұЯONФЪЦұПЯABөДПВ·ҪЈ®
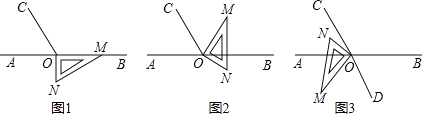
ЈЁ1Ј©Ҫ«Нј1ЦРөДИэҪЗ°еИЖөгOДжКұХлРэЧӘЦБНј2Ј¬К№Т»ұЯOMФЪЎПBOCөДДЪІҝЈ¬ЗТЗЎәГЖҪ·ЦЎПBOCЈ¬ОКЈәЦұПЯONКЗ·сЖҪ·ЦЎПAOCЈҝЗлЛөГчАнУЙЈ»
ЈЁ2Ј©Ҫ«Нј1ЦРөДИэҪЗ°еИЖөгO°ҙГҝГл5ЎгөДЛЩ¶ИСШДжКұХл·ҪПтРэЧӘТ»ЦЬЈ¬ФЪРэЧӘөД№эіМЦРЈ¬өЪtГлКұЈ¬ЦұПЯONЗЎәГЖҪ·ЦИсҪЗЎПAOCЈ¬ФтtөДЦөОӘЎЎ ЈЁЦұҪУРҙіцҪб№ыЈ©Ј»
ЈЁ3Ј©Ҫ«Нј1ЦРөДИэҪЗ°еИЖөгOЛіКұХлРэЧӘЦБНј3Ј¬К№ONФЪЎПAOCөДДЪІҝЈ¬ODОӘЎПBOMЖҪ·ЦПЯЈ®ЗлМҪҫҝЈәЎПMODУлЎПNOCЦ®јдөДКэБҝ№ШПөЈ¬ІўЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ТСЦӘПЯ¶О![]() Ј¬өг
Ј¬өг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() Ј¬өг
Ј¬өг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() Ј¬ИзНј1ЛщКҫ.
Ј¬ИзНј1ЛщКҫ.
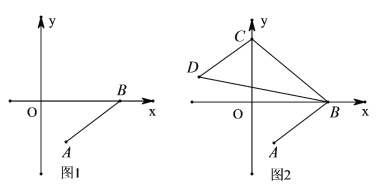
(1)ЖҪТЖПЯ¶О![]()
![]() өҪПЯ¶О
өҪПЯ¶О![]()
![]() Ј¬К№өг
Ј¬К№өг![]() өД¶ФУҰөгОӘЈ¬өг
өД¶ФУҰөгОӘЈ¬өг![]() өД¶ФУҰөгОӘ
өД¶ФУҰөгОӘ![]() Ј¬Ифөг
Ј¬Ифөг![]() өДЧшұкОӘ
өДЧшұкОӘ![]() Ј¬Зуөг
Ј¬Зуөг![]() өДЧшұкЈ»
өДЧшұкЈ»
(2)ЖҪТЖПЯ¶О![]()
![]() өҪПЯ¶О
өҪПЯ¶О![]()
![]() Ј¬К№өг
Ј¬К№өг![]() ФЪ
ФЪ![]() ЦбөДХэ°лЦбЙПЈ¬өг
ЦбөДХэ°лЦбЙПЈ¬өг![]() ФЪөЪ¶юПуПЮДЪ(
ФЪөЪ¶юПуПЮДЪ(![]() Ул
Ул![]() ¶ФУҰЈ¬
¶ФУҰЈ¬ ![]() Ул
Ул![]() ¶ФУҰ)Ј¬Б¬ҪУ
¶ФУҰ)Ј¬Б¬ҪУ![]() ИзНј2ЛщКҫ.Иф
ИзНј2ЛщКҫ.Иф![]() ұнКҫЎчBCDөДГж»э)Ј¬Зуөг
ұнКҫЎчBCDөДГж»э)Ј¬Зуөг![]() Ўў
Ўў![]() өДЧшұкЈ»
өДЧшұкЈ»
(3)ФЪ(2)өДМхјюПВЈ¬ФЪ![]() ЦбЙПКЗ·сҙжФЪТ»өг
ЦбЙПКЗ·сҙжФЪТ»өг![]() Ј¬К№
Ј¬К№![]() ЈҝИфҙжФЪЈ¬Зуіцөг
ЈҝИфҙжФЪЈ¬Зуіцөг![]() өДЧшұк,
өДЧшұк,
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬AЎўBОӘxЦбЙПБҪөгЈ¬CЎўDОӘyЦбЙПөДБҪөгЈ¬ҫӯ№эөгAЎўCЎўBөДЕЧОпПЯөДТ»Іҝ·Цc1Улҫӯ№эөгAЎўDЎўBөДЕЧОпПЯөДТ»Іҝ·Цc2ЧйәПіЙТ»Мх·вұХЗъПЯЈ¬ОТГЗ°СХвМх·вұХЗъПЯіЙОӘЎ°ө°ПЯЎұЈ®ТСЦӘөгCөДЧшұкОӘЈЁ0Ј¬©Ғ![]() Ј©Ј¬өгMКЗЕЧОпПЯC2Јәy=mx2©Ғ2mx©Ғ3mЈЁmЈј0Ј©өД¶ҘөгЈ®
Ј©Ј¬өгMКЗЕЧОпПЯC2Јәy=mx2©Ғ2mx©Ғ3mЈЁmЈј0Ј©өД¶ҘөгЈ®
ЈЁ1Ј©ЗуAЎўBБҪөгөДЧшұкЈ»
ЈЁ2Ј©Ў°ө°ПЯЎұФЪөЪЛДПуПЮЙПКЗ·сҙжФЪТ»өгPЈ¬К№өГЎчPBCөДГж»эЧоҙуЈҝИфҙжФЪЈ¬ЗуіцЎчPBCГж»эөДЧоҙуЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ»
ЈЁ3Ј©өұЎчBDMОӘЦұҪЗИэҪЗРОКұЈ¬ЗуmөДЦөЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ABCDЦРЈ¬BDЎНADЈ¬ЎПA=45ЎгЈ¬EЎўF·ЦұрКЗABЈ¬CDЙПөДөгЈ¬ЗТBE=DFЈ¬Б¬ҪУEFҪ»BDУЪOЈ®

ЈЁ1Ј©ЗуЦӨЈәBO=DOЈ»
ЈЁ2Ј©ИфEFЎНABЈ¬СУіӨEFҪ»ADөДСУіӨПЯУЪGЈ¬өұFG=1КұЈ¬ЗуADөДіӨЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
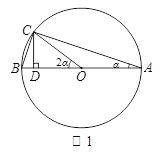
ЎҫМвДҝЎҝЎҫФД¶БС§П°Ўҝ БхАПКҰМбіцХвСщТ»ёцОКМвЈәТСЦӘҰБОӘИсҪЗЈ¬ЗТtanҰБ=![]() Ј¬Зуsin2ҰБөДЦөЈ®
Ј¬Зуsin2ҰБөДЦөЈ®
РЎҫкКЗХвСщҪвҫцөДЈә
ИзНј1Ј¬ФЪЎСOЦРЈ¬ABКЗЦұҫ¶Ј¬өгCФЪЎСOЙПЈ¬ЎПBAC=ҰБЈ¬ЛщТФЎПACB=90ЎгЈ¬tanҰБ=![]() =
=![]() Ј®
Ј®
ТЧөГЎПBOC=2ҰБЈ®ЙиBC=xЈ¬ФтAC=3xЈ¬ФтAB=![]() xЈ®ЧчCDЎНABУЪDЈ¬ЗуіцCD= ЈЁУГә¬xөДКҪЧУұнКҫЈ©Ј¬ҝЙЗуөГsin2ҰБ=
xЈ®ЧчCDЎНABУЪDЈ¬ЗуіцCD= ЈЁУГә¬xөДКҪЧУұнКҫЈ©Ј¬ҝЙЗуөГsin2ҰБ=![]() = Ј®
= Ј®
ЎҫОКМвҪвҫцЎҝ
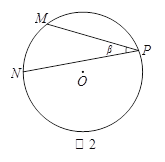
ТСЦӘЈ¬ИзНј2Ј¬өгMЎўNЎўPОӘФІOЙПөДИэөгЈ¬ЗТЎПP=ҰВЈ¬tanҰВ =![]() Ј¬Зуsin2ҰВөДЦөЈ®
Ј¬Зуsin2ҰВөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ№ЫІмПВБРФЛЛгЈә81ЈҪ8Ј¬82ЈҪ64Ј¬83ЈҪ512Ј¬84ЈҪ4 096Ј¬85ЈҪ32 768Ј¬86ЈҪ262 144Ј¬ЎӯЈ¬Фт81Ј«82Ј«83Ј«84Ј«ЎӯЈ«82 018Ј«82 019өДәНөДёцО»КэЧЦКЗ____Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦұПЯy1ЈҪ2xУлЦұПЯy2ЈҪ©Ғ2x+4ПаҪ»УЪөгAЈ®ТФПВҪбВЫЈә
ўЩөгAөДЧшұкОӘAЈЁ1Ј¬2Ј©Ј»ўЪөұxЈҪ1КұЈ¬БҪёцәҜКэЦөПаөИЈә
ўЫөұxЈј1КұЈ¬y1Јјy2Ј»ЎЎЎЎўЬЦұПЯy1ЈҪ2xУлЦұПЯy2ЈҪ©Ғ2x+4ФЪЖҪГжЦұҪЗЧшұкПөЦРөДО»ЦГ№ШПөКЗЖҪРРЈ®ЖдЦРХэИ·өДёцКэУРЈЁЎЎЎЎЈ©ёцЈ®
A. 4B. 3C. 2D. 1
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com