
【题目】已知数轴上A,B两点对应的数分别为a和b,且a,b满足等式![]() ,p为数轴上一动点,对应的数为x.
,p为数轴上一动点,对应的数为x.
![]() ______,
______,![]() ______,线段
______,线段![]() ______.
______.
![]() 数轴上是否存在点p,使
数轴上是否存在点p,使![]() ?若存在,求出x的值;若不存在,请说明理由.
?若存在,求出x的值;若不存在,请说明理由.
![]() 在
在![]() 的条件下,若M,N分别是线段AB,PB的中点,试求线段MN的长.
的条件下,若M,N分别是线段AB,PB的中点,试求线段MN的长.
【答案】(1)-9;7;(2)15;(3)6或12.
【解析】
![]() 根据非负数的和等于零,可得每个非负数同时为零,根据数轴上两点间的距离是大数减小数,可得答案;
根据非负数的和等于零,可得每个非负数同时为零,根据数轴上两点间的距离是大数减小数,可得答案;
![]() 根据线段的和差,可得关于PB的方程,根据解方程,可得PB的长,根据数轴上的两点间的距离,可得x;
根据线段的和差,可得关于PB的方程,根据解方程,可得PB的长,根据数轴上的两点间的距离,可得x;
![]() 根据线段中点的性质,可得MB,NB,根据线段的和差,可得答案.
根据线段中点的性质,可得MB,NB,根据线段的和差,可得答案.
解:![]() 由
由![]() ,得
,得
![]() ,
,![]() .
.
解得![]() ,
,![]() .
.
线段![]() ;
;
![]() 当P在AB上时,
当P在AB上时,![]() ,即
,即![]() ,
,
即![]() ,
,
![]() ,
,
解得![]() ;
;
当P在线段AB的延长线上时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 当P在AB上时,如图1;
当P在AB上时,如图1;
![]() ,
,
点M、点N分别是线段AB,PB的中点,得
![]() ,
,![]() .
.
由线段的和差,得
![]() ;
;
当P在AB的延长线上时,如图2;
 ,
,
点M、点N分别是线段AB,PB的中点,得
![]() ,
,![]() .
.
由线段的和差,得
![]() .
.
综上所述:MN的长为6或12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某企业对每个员工在当月生产某种产品的件数统计如下:设产品件数为x(单位:件),企业规定:当x<15时为不称职;当15≤x<20时为基本称职;当20≤x<25为称职;当x≥25时为优秀.解答下列问题
(1)试求出优秀员工人数所占百分比;
(2)计算所有优秀和称职的员工中月产品件数的中位数和众数;
(3)为了调动员工的工作积极性,企业决定制定月产品件数奖励标准,凡达到或超过这个标准的员工将受到奖励.如果要使得所有优秀和称职的员工中至少有一半能获奖,你认为这个奖励标准应定为多少件合适?简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式: ![]() ,
, ![]() ,给出定义如下:
,给出定义如下:
我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
, ![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
, ![]() ),如:数对(
),如:数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)判断数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;
(2)若(![]() ,
, ![]() )是“共生有理数对”,求
)是“共生有理数对”,求![]() 的值;
的值;
(3)若(![]() ,
, ![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
, ![]() ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;
(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.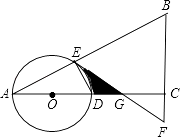
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加一个条件使△ABC≌△DCB,下列添加的条件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,二次函数y=﹣ ![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.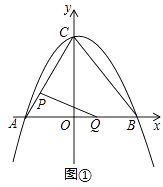
(1)填空:b= , c=;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣ ![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个函数的图象如图所示,给出以下结论:①当x=0时,函数值最大;②当0<x<2时,函数y随x的增大而减小;③当x<0时,函数y随x的增大而增大;④存在0<a<1,当x=a时,函数值为0.其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com