
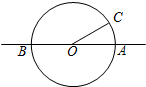
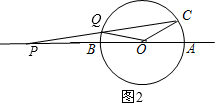
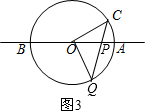
 如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在圆O上,且∠AOC=30°,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q.如果QP=QO,则∠OCP的度数是
如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在圆O上,且∠AOC=30°,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q.如果QP=QO,则∠OCP的度数是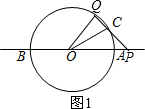


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
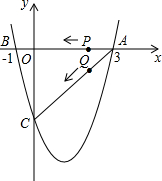 如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:
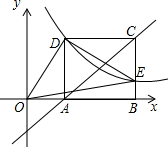 如图,已知正方形ABCD的边长为2,双曲线y=
如图,已知正方形ABCD的边长为2,双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是随机抽查某校40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该校4000名同学一周参加体育锻炼时间达到9小时以上(含9小时)的人数是
如图是随机抽查某校40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该校4000名同学一周参加体育锻炼时间达到9小时以上(含9小时)的人数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com